Quad#
表示平面中的四边形(也叫“矩形”或“四边形”),由四个 Point 对象组成,分别是 ul、ur、ll、lr(分别称为左上角、右上角、左下角、右下角)。
四边形可以 通过 文本搜索方法获得(如: Page.search_for()),并且 用于 定义文本标记注释(参见例如: Page.add_squiggly_annot() 等),以及在多个绘图方法中使用(如: Page.draw_quad() / Shape.draw_quad() , Page.draw_oval() / Shape.draw_quad())。
备注
如果矩形的角点经过 旋转 、 缩放 或 平移 的 Matrix 变换,则结果四边形是 矩形 (即与矩形全等),即所有角点仍然形成 90 度角。属性
Quad.is_rectangular用于检查四边形是否可以视为这种变换的结果。不是所有矩阵都适用:例如,剪切矩阵会产生平行四边形,而不可逆矩阵则会生成“退化”四边形,如三角形或直线。
属性
Quad.rect获取最小的包含矩形。反之,矩形现在具有属性Rect.quad,即IRect.quad,用于获取其相应的四边形版本。
方法 / 属性 |
简短描述 |
|---|---|
使用矩阵进行变换 |
|
使用点和矩阵进行变换 |
|
左上点 |
|
右上点 |
|
左下点 |
|
右下点 |
|
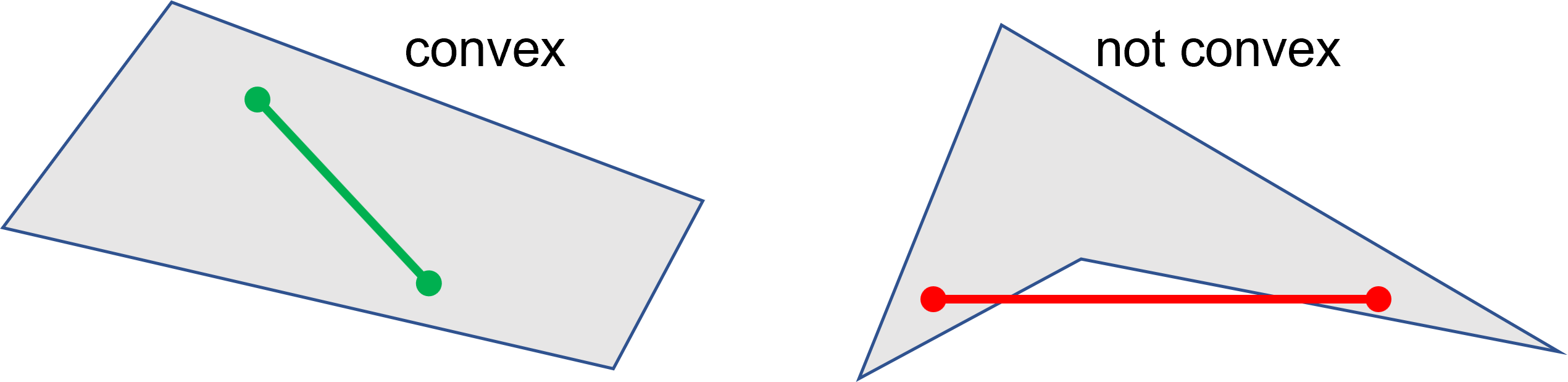
如果四边形是凸集,则为真 |
|
如果四边形为空集,则为真 |
|
如果四边形全等于矩形,则为真 |
|
包含四边形的最小 Rect |
|
最长宽度值 |
|
最长高度值 |
类 API
- class Quad#
- __init__(self)#
- __init__(self, ul, ur, ll, lr)#
- __init__(self, quad)#
- __init__(self, sequence)#
重载构造函数:”ul”、”ur”、”ll”、”lr” 代表
point_like对象(四个角点),”sequence” 是包含四个point_like对象的 Python 序列。如果指定了 “quad”,构造函数会创建一个 新的副本。
如果没有参数,则会创建一个由 4 个 Point(0, 0) 组成的四边形。
- transform(matrix)#
通过矩阵变换修改四边形,变换其每个角点。
- 参数:
matrix (matrix_like) – 要应用的矩阵。
- morph(fixpoint, matrix)#
(新版本 1.17.0 引入) 使用类似矩阵的对象,通过指定固定点对四边形进行变换。
- 参数:
fixpoint (point_like) – 固定点。
matrix (matrix_like) – 要应用的矩阵。
- 返回:
一个新的四边形(如果是无限四边形则不进行操作)。
- is_convex#
新版本 1.16.1 引入
检查四边形的任意两点之间的连接线上的所有点是否也属于四边形。
- Type:
bool
- is_empty#
如果包围的区域为零,则为真,这意味着至少三个角点在同一条线上。如果为假,四边形可能仍然是退化的,或者根本不像四边形(如三角形、平行四边形、梯形等)。
- Type:
bool
- is_rectangular#
如果所有角度为 90 度,则为真。这意味着四边形是 凸的且不为空。
- Type:
bool
- width#
上边和下边的最大长度。
- Type:
float
- height#
左边和右边的最大长度。
- Type:
float
Represents a four-sided mathematical shape (also called “quadrilateral” or “tetragon”) in the plane, defined as a sequence of four Point objects ul, ur, ll, lr (conveniently called upper left, upper right, lower left, lower right).
Quads can be obtained as results of text search methods (Page.search_for()), and they are used to define text marker annotations (see e.g. Page.add_squiggly_annot() and friends), and in several draw methods (like Page.draw_quad() / Shape.draw_quad(), Page.draw_oval()/ Shape.draw_quad()).
备注
If the corners of a rectangle are transformed with a rotation, scale or translation Matrix, then the resulting quad is rectangular (= congruent to a rectangle), i.e. all of its corners again enclose angles of 90 degrees. Property
Quad.is_rectangularchecks whether a quad can be thought of being the result of such an operation.This is not true for all matrices: e.g. shear matrices produce parallelograms, and non-invertible matrices deliver “degenerate” tetragons like triangles or lines.
Attribute
Quad.rectobtains the enveloping rectangle. Vice versa, rectangles now have attributesRect.quad, resp.IRect.quadto obtain their respective tetragon versions.
Methods / Attributes |
Short Description |
|---|---|
transform with a matrix |
|
transform with a point and matrix |
|
upper left point |
|
upper right point |
|
lower left point |
|
lower right point |
|
true if quad is a convex set |
|
true if quad is an empty set |
|
true if quad is congruent to a rectangle |
|
smallest containing Rect |
|
the longest width value |
|
the longest height value |
Class API
评论#
Remark
此类遵循序列协议,因此也可以通过其索引来处理组件。另请参阅 在 PyMuPDF 中使用 Python 序列作为参数。
This class adheres to the sequence protocol, so components can be dealt with via their indices, too. Also refer to 在 PyMuPDF 中使用 Python 序列作为参数.
代数和包含检查#
Algebra and Containment Checks
从 v1.19.6 开始,四边形(quads)可以像其他几何对象一样用于代数表达式 – 相关的限制已被取消。特别地,现在所有以下的包含关系检查组合都可以使用:
{Point | IRect | Rect | Quad} in {IRect | Rect | Quad}
请注意以下有趣的细节:
对于矩形,只有其左上角的点属于它。自 v1.19.0 起,矩形被定义为“开区间”,即其底边和右边不属于矩形 — 包括相应的角点。但对于四边形,概念中没有类似于“开区间”的定义,因此我们有以下令人惊讶的结论:
>>> rect.br in rect
False
>>> # 但:
>>> rect.br in rect.quad
True
Starting with v1.19.6, quads can be used in algebraic expressions like the other geometry object – the respective restrictions have been lifted. In particular, all the following combinations of containment checking are now possible:
{Point | IRect | Rect | Quad} in {IRect | Rect | Quad}
Please note the following interesting detail:
For a rectangle, only its top-left point belongs to it. Since v1.19.0, rectangles are defined to be “open”, such that its bottom and its right edge do not belong to it – including the respective corners. But for quads there exists no such notion like “openness”, so we have the following somewhat surprising implication:
>>> rect.br in rect
False
>>> # but:
>>> rect.br in rect.quad
True