课后习题与问题#
Homework Problems and Questions
第 8.1 节#
SECTION 8.1
R1. 消息机密性与消息完整性之间有什么区别?是否可以在没有完整性的情况下实现机密性?是否可以在没有机密性的情况下实现完整性?请说明你的理由。
R2. 互联网实体(路由器、交换机、DNS 服务器、Web 服务器、用户端系统等)经常需要进行安全通信。请给出三个希望进行安全通信的互联网实体配对的具体示例。
R1. What are the differences between message confidentiality and message integrity? Can you have confidentiality without integrity? Can you have integrity without confidentiality? Justify your answer.
R2. Internet entities (routers, switches, DNS servers, Web servers, user end systems, and so on) often need to communicate securely. Give three specific example pairs of Internet entities that may want secure communication.
第 8.2 节#
SECTION 8.2
R3. 从服务的角度来看,对称密钥系统与公钥系统之间有什么重要区别?
R4. 假设一个入侵者拥有一条加密消息及该消息的解密版本。入侵者可以发动仅密文攻击、已知明文攻击或选择明文攻击吗?
R5. 考虑一个 8 位分组加密器。该加密器有多少种可能的输入分组?有多少种可能的映射?如果我们将每种映射视为一个密钥,那么该加密器有多少种可能的密钥?
R6. 假设 N 个人希望使用对称密钥加密与另外 N−1 个人进行通信。任何两个用户 i 和 j 之间的通信对该组中的所有其他人都是可见的,且该组中的任何其他人都不应该能够解密他们的通信。该系统总共需要多少个密钥?现在假设使用的是公钥加密。在这种情况下需要多少个密钥?
R7. 假设 n=10,000,a=10,023,b=10,004。使用模运算的恒等式心算计算 (a⋅b)mod n。
R8. 假设你想通过加密对应于消息的十进制数字来加密消息 10101111。这个十进制数字是多少?
R3. From a service perspective, what is an important difference between a symmetric-key system and a public-key system?
R4. Suppose that an intruder has an encrypted message as well as the decrypted version of that message. Can the intruder mount a ciphertext-only attack, a known-plaintext attack, or a chosen-plaintext attack?
R5. Consider an 8-block cipher. How many possible input blocks does this cipher have? How many possible mappings are there? If we view each mapping as a key, then how many possible keys does this cipher have?
R6. Suppose N people want to communicate with each of N−1 other people using symmetric key encryption. All communication between any two people, i and j, is visible to all other people in this group of N, and no other person in this group should be able to decode their communication. How many keys are required in the system as a whole? Now suppose that public key encryption is used. How many keys are required in this case?
R7. Suppose n=10,000, a=10,023, and b=10,004. Use an identity of modular arithmetic to calculate in your head (a⋅b)mod n.
R8. Suppose you want to encrypt the message 10101111 by encrypting the decimal number that corresponds to the message. What is the decimal number?
第 8.3–8.4 节#
SECTIONS 8.3–8.4
R9. 在哪些方面,哈希比校验和(例如 Internet 校验和)能提供更好的消息完整性检查?
R10. 是否可以“解密”消息的哈希值以获取原始消息?请解释你的回答。
R11. 考虑 MAC 算法的一种变体(图 8.9),其中发送方发送 (m, H(m)+s),其中 H(m)+s 是 H(m) 和 s 的连接。这种变体是否有缺陷?为什么或为什么没有?
R12. 对于一个签名的文档,可验证性和不可伪造性意味着什么?
R13. 在哪些方面,公钥加密的消息哈希比公钥加密的消息本身能提供更好的数字签名?
R14. 假设 certifier.com 为 foo.com 创建了一个证书。通常情况下,整个证书会用 certifier.com 的公钥加密。对还是错?
R15. 假设 Alice 有一条准备发送给任何请求者的消息。成千上万的人希望获取 Alice 的消息,但每个人都希望确保消息的完整性。在这种情境下,你认为基于 MAC 的完整性机制更合适,还是基于数字签名的机制更合适?为什么?
R16. 在终端身份验证协议中,随机数(nonce)的作用是什么?
R17. 所谓随机数是“一生中仅使用一次的值”是什么意思?这里的“一生”指的是谁的生命周期?
R18. 基于 HMAC 的消息完整性方案是否容易受到重放攻击?如果是,如何将随机数纳入该方案以消除这种易受攻击性?
R9. In what way does a hash provide a better message integrity check than a checksum (such as the Internet checksum)?
R10. Can you “decrypt” a hash of a message to get the original message? Explain your answer. R11. Consider a variation of the MAC algorithm (Figure 8.9 ) where the sender sends (m, H(m)+s), where H(m)+s is the concatenation of H(m) and s. Is this variation flawed? Why or why not?
R12. What does it mean for a signed document to be verifiable and nonforgeable?
R13. In what way does the public-key encrypted message hash provide a better digital signature than the public-key encrypted message?
R14. Suppose certifier.com creates a certificate for foo.com. Typically, the entire certificate would be encrypted with certifier.com’s public key. True or false?
R15. Suppose Alice has a message that she is ready to send to anyone who asks. Thousands of people want to obtain Alice’s message, but each wants to be sure of the integrity of the message. In this context, do you think a MAC-based or a digital-signature-based integrity scheme is more suitable? Why?
R16. What is the purpose of a nonce in an end-point authentication protocol?
R17. What does it mean to say that a nonce is a once-in-a-lifetime value? In whose lifetime?
R18. Is the message integrity scheme based on HMAC susceptible to playback attacks? If so, how can a nonce be incorporated into the scheme to remove this susceptibility?
第 8.5–8.8 节#
SECTIONS 8.5–8.8
R19. 假设 Bob 收到来自 Alice 的一条 PGP 消息。Bob 如何确定消息确实是 Alice 创建的(而不是例如 Trudy)?PGP 是否使用 MAC 来保证消息完整性?
R20. 在 SSL 记录中,有一个用于 SSL 序列号的字段。对还是错?
R21. 在 SSL 握手中,随机数的作用是什么?
R22. 假设一个 SSL 会话使用带有 CBC 的分组加密器。对还是错:服务器以明文形式将 IV 发送给客户端。
R23. 假设 Bob 发起到 Trudy 的 TCP 连接,而 Trudy 假装是 Alice。在握手过程中,Trudy 将 Alice 的证书发送给 Bob。在 SSL 握手算法的哪个步骤中,Bob 会发现他并未与 Alice 通信?
R24. 考虑从主机 A 向主机 B 发送一个数据包流,并使用 IPsec。通常,每个发送的数据包都会建立一个新的 SA。对还是错?
R25. 假设 TCP 在总部和分支机构之间通过 IPsec 运行(参见 图 8.28)。如果 TCP 重新传输相同的数据包,那么由 R1 发送的两个相应的数据包在 ESP 头中的序列号是否相同?对还是错?
R26. IKE SA 和 IPsec SA 是同一个东西。对还是错?
R27. 考虑 802.11 的 WEP。假设数据是 10101100,密钥流是 1111000。结果密文是多少?
R28. 在 WEP 中,IV 在每一帧中都以明文形式发送。对还是错?
R19. Suppose that Bob receives a PGP message from Alice. How does Bob know for sure that Alice created the message (rather than, say, Trudy)? Does PGP use a MAC for message integrity?
R20. In the SSL record, there is a field for SSL sequence numbers. True or false? R21. What is the purpose of the random nonces in the SSL handshake?
R22. Suppose an SSL session employs a block cipher with CBC. True or false: The server sends to the client the IV in the clear.
R23. Suppose Bob initiates a TCP connection to Trudy who is pretending to be Alice. During the handshake, Trudy sends Bob Alice’s certificate. In what step of the SSL handshake algorithm will Bob discover that he is not communicating with Alice?
R24. Consider sending a stream of packets from Host A to Host B using IPsec. Typically, a new SA will be established for each packet sent in the stream. True or false?
R25. Suppose that TCP is being run over IPsec between headquarters and the branch office in Figure 8.28 . If TCP retransmits the same packet, then the two corresponding packets sent by R1 packets will have the same sequence number in the ESP header. True or false?
R26. An IKE SA and an IPsec SA are the same thing. True or false?
R27. Consider WEP for 802.11. Suppose that the data is 10101100 and the keystream is 1111000. What is the resulting ciphertext?
R28. In WEP, an IV is sent in the clear in every frame. True or false?
第 8.9 节#
SECTION 8.9
R29. 有状态数据包过滤器维护两个数据结构。请列出它们并简要说明它们的作用。
R30. 考虑一个传统(无状态)数据包过滤器。该过滤器可以基于 TCP 标志位以及其他报头字段过滤数据包。对还是错?
R31. 在传统的数据包过滤器中,每个接口都可以有自己的访问控制列表。对还是错?
R32. 为什么应用网关必须与路由器过滤器配合使用才能有效?
R33. 基于签名的 IDS 和 IPS 会检查 TCP 和 UDP 段的有效负载。对还是错?
R29. Stateful packet filters maintain two data structures. Name them and briefly describe what they do.
R30. Consider a traditional (stateless) packet filter. This packet filter may filter packets based on TCP flag bits as well as other header fields. True or false?
R31. In a traditional packet filter, each interface can have its own access control list. True or false?
R32. Why must an application gateway work in conjunction with a router filter to be effective?
R33. Signature-based IDSs and IPSs inspect into the payloads of TCP and UDP segments. True or false?
习题#
Problems
P1. 使用 图 8.3 中的单表代换密码对消息“This is an easy problem.”进行编码。解码消息“rmij’u uamu xyj”。
P2. 证明 Trudy 的已知明文攻击,即她知道七个字母的(密文,明文)对,在 第 8.2.1 节 中的示例中将待检验的可能替换数减少了约 10^9。
P3. 考虑 图 8.4 所示的多表代换系统。一个能够获取消息“The quick brown fox jumps over the lazy dog.”加密结果的选择明文攻击是否足以解密所有消息?请说明原因。
P4. 考虑 图 8.5 中的分组加密算法。假设每个分组加密器 Ti 仅反转八位输入比特的顺序(例如,11110000 变成 00001111)。进一步假设 64 位置乱器不修改任何比特(即第 m 位输出等于第 m 位输入)。(a)当 n=3 且原始 64 位输入为 10100000 重复八次时,输出值是多少?(b)重复 (a) 部分,但将原始 64 位输入的最后一位从 0 改为 1。(c)重复 (a) 和 (b),但现在假设 64 位置乱器反转 64 位的顺序。
P5. 考虑 图 8.5 中的分组加密算法。对于给定“密钥”,Alice 和 Bob 需要保留八个表格,每个为 8×8 比特。Alice(或 Bob)要存储所有八个表需要多少比特?与存储一个完整的 64 位分组加密表相比,这个数目如何?
P6. 考虑 表 8.1 中的 3 位分组加密器。假设明文为 100100100。(a)最初假设未使用 CBC。结果密文是什么?(b)假设 Trudy 嗅探到了密文,并知道使用了一个不带 CBC 的 3 位分组加密器(但不知道具体加密器),她能推测出什么?(c)现在假设使用了 CBC,且 IV=111。结果密文是什么?
P7. (a)使用 RSA,选择 p=3 和 q=11,并将单词“dog”加密,每个字母单独加密。应用解密算法恢复原始明文消息。(b)重复 (a),但现在将“dog”作为一个整体消息 m 加密。
P8. 考虑 p=5 和 q=11 的 RSA 算法。
n 和 z 的值是多少?
令 e=3。为什么这是一个可接受的 e 值?
找出满足 de=1 (mod z) 且 d<160 的 d 值。
使用密钥 (n, e) 加密消息 m=8。设 c 为对应的密文。展示所有计算过程。提示:为简化计算,使用恒等式 [ (a mod n)⋅(b mod n)]mod n=(a⋅b)modn
P9. 本题探讨 Diffie-Hellman(DH)公钥加密算法,它允许两个实体达成共享密钥。DH 算法使用一个大素数 p 和另一个小于 p 的大数 g。p 和 g 是公开的(攻击者也知道)。Alice 和 Bob 各自独立选择私钥 SA 和 SB。Alice 通过将 g 的 SA 次幂对 p 取模计算出其公钥 TA,Bob 类似地计算 TB。然后 Alice 和 Bob 交换各自的公钥。Alice 通过将 TB 的 SA 次幂对 p 取模得到共享密钥 S,Bob 则通过将 TA 的 SB 次幂对 p 取模得到共享密钥 S’。
证明 Alice 和 Bob 得到的对称密钥相同,即 S=S’。
若 p=11 且 g=2,Alice 和 Bob 的私钥分别为 SA=5 和 SB=12。计算 Alice 和 Bob 的公钥 TA 和 TB,展示所有过程。
在 (b) 的基础上,计算共享密钥 S,展示所有过程。
绘制时间图,展示 Trudy 作为中间人攻击 Diffie-Hellman 的过程。图中应包含 Alice、Bob 和攻击者 Trudy 三条垂直线。
P10. 假设 Alice 想使用对称密钥密码(会话密钥 \(K_S\))与 Bob 通信。在 第 8.2 节 中我们了解到如何使用公钥加密分发会话密钥。本题探讨如何在不使用公钥加密的前提下通过密钥分发中心(KDC)分发会话密钥。KDC 与每个注册用户共享一个独特的对称密钥。对于 Alice 和 Bob,分别记为 \(K_{A-KDC}\) 和 \(K_{B-KDC}\)。设计一个三条消息的方案来分发 \(K_S\):Alice→KDC、KDC→Alice、Alice→Bob。第一条消息为 \(K_{A-KDC}\) (A, B)。请使用所给符号回答以下问题。
第二条消息是什么?
第三条消息是什么?
P11. 计算一个不同于 图 8.8 中两个消息的第三个消息,但其校验和相同。
P12. 假设 Alice 和 Bob 共享两个秘密密钥:一个认证密钥 S1 和一个对称加密密钥 S2。扩展 图 8.9 以同时提供完整性和机密性。
P13. 在 BitTorrent P2P 文件分发协议(参见 第 2 章)中,种子将文件分块,其他对等体相互转发这些块。若无任何保护,攻击者可以伪装成正常节点向少数节点发送伪造块,这些节点再转发给其他节点,造成大面积感染。因此,BitTorrent 必须有机制让节点验证块的完整性。假设节点从完全可信源获得 .torrent 文件。请描述一个简单方案用于块完整性验证。
P14. OSPF 路由协议使用 MAC 而非数字签名提供消息完整性。你认为为什么选择 MAC 而不是数字签名?
P15. 考虑 图 8.18 中的认证协议,Alice 向 Bob 认证,协议被认为是安全的。现在假设 Bob 同时也要向 Alice 认证。给出一个场景,使得 Trudy 可假冒 Alice 向 Bob 完成认证。(提示:注意协议的两个实例可能交错进行,尤其关注双方使用 nonce 的方式,若处理不当可能被恶意利用。)
P16. 自然的问题是能否使用 nonce 和公钥密码解决 第 8.4 节 中的端点认证问题。考虑如下协议:(1) Alice 发送“I am Alice”给 Bob;(2) Bob 生成 nonce R 并发送给 Alice;(3) Alice 用私钥加密 R 并发回;(4) Bob 用 Alice 的公钥解密,得出 R,从而完成认证。
使用教材中使用的公钥/私钥符号绘制此协议图。
假设不使用证书。描述 Trudy 如何通过拦截 Alice 的消息并假冒其身份成为“中间女”。
P17. 图 8.19 展示了 Alice 使用 PGP 提供机密性、认证和完整性所需的操作。请绘制 Bob 在接收到 Alice 的数据包后需执行的对应操作图。
P18. 假设 Alice 要向 Bob 发送电子邮件。Bob 拥有公私钥对 (KB+, KB−),Alice 拥有 Bob 的证书,但没有自己的密钥对。Alice、Bob 和所有人共享同一个散列函数 H(⋅)。
在此情境中,是否可以设计一种方案让 Bob 验证消息来自 Alice?若可,请用框图展示 Alice 和 Bob 的操作。
是否可以设计一种方案让消息从 Alice 发送到 Bob 时具备机密性?若可,请用框图展示。
P19. 考虑下方 SSL 会话中 Wireshark 的输出。
Wireshark 包 112 是由客户端还是服务器发送?
服务器的 IP 地址和端口号是多少?
假设无丢包和重传,客户端下一个 TCP 段的序号是多少?
包 112 含有多少个 SSL 记录?
包 112 是否包含主密钥、加密主密钥或都不包含?
假设握手类型字段为 1 字节,每个长度字段为 3 字节,主密钥(或加密主密钥)的首尾字节是什么?
客户端加密握手消息考虑了多少 SSL 记录?
服务器加密握手消息考虑了多少 SSL 记录?
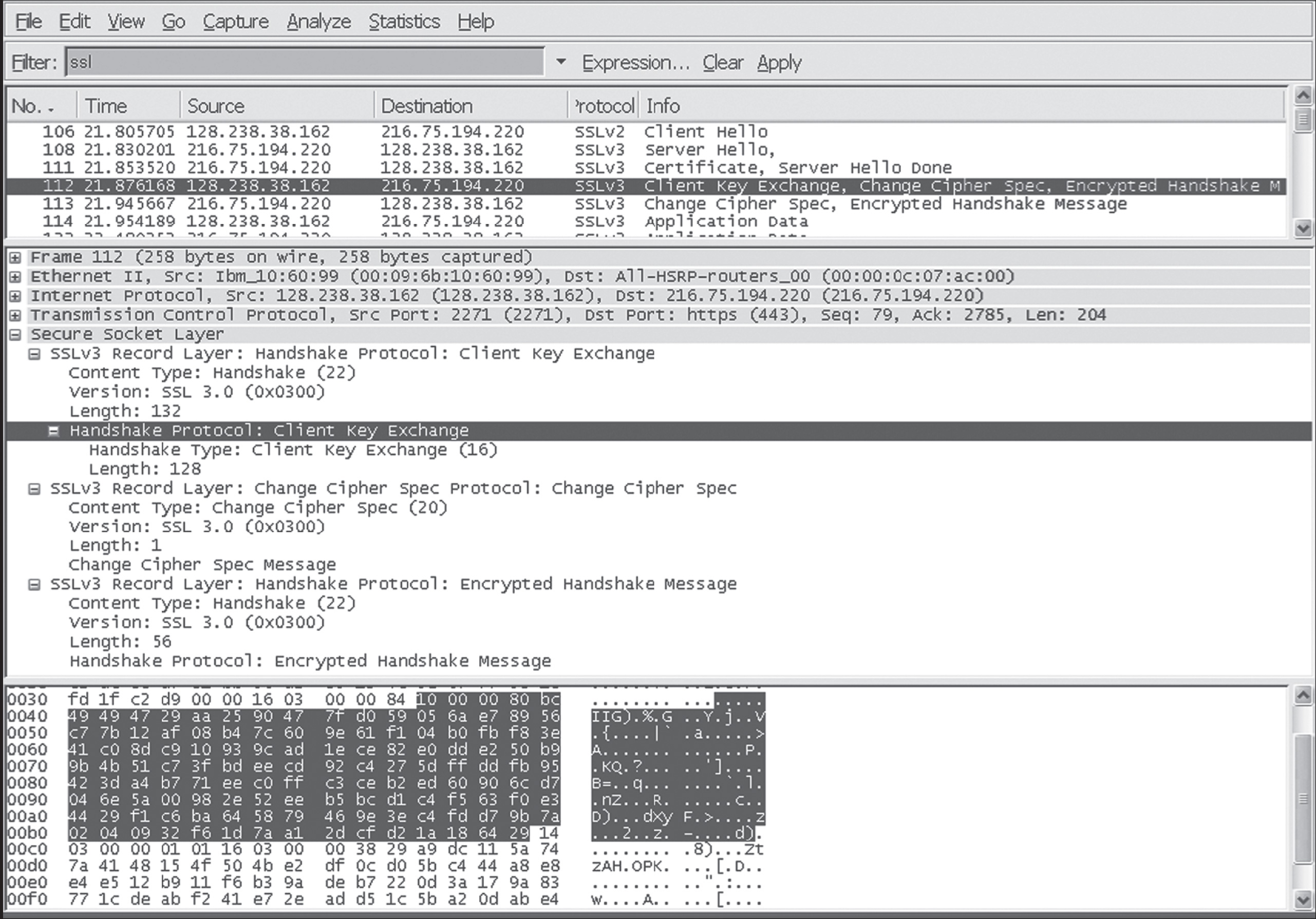
(Wireshark 截图由 Wireshark 基金会授权转载。)
P20. 在 第 8.6.1 节 中指出,如果没有序号,Trudy 可通过互换 TCP 段对 SSL 会话进行攻击。Trudy 能否通过删除一个 TCP 段进行类似攻击?她需做什么才能成功?其后果是什么?
P21. 假设 Alice 和 Bob 正通过 SSL 会话通信。攻击者插入一个伪造的 TCP 段,具有正确的 TCP 校验和、序号、IP 地址和端口。接收方的 SSL 是否会接受此包并将其有效载荷交给应用程序?为什么?
P22. 以下判断题与 图 8.28 有关:
当 172.16.1/24 的主机向 Amazon.com 服务器发送数据报时,路由器 R1 将使用 IPsec 加密数据报。
当 172.16.1/24 的主机向 172.16.2/24 的主机发送数据报时,R1 会修改 IP 数据报的源地址和目标地址。
假设一个 TCP 连接从 172.16.1/24 的主机发起至 172.16.2/24 的 Web 服务器。作为连接的一部分,R1 发送的所有数据报左侧 IPv4 头字段中协议号为 50。
从 172.16.1/24 的主机向 172.16.2/24 的主机发送 TCP 段。如果确认丢失导致 TCP 重传,R1 会因 IPsec 使用序号而不重发该段。
P23. 考虑 图 8.28 中的示例。假设 Trudy 为中间人,能向 R1 到 R2 的数据报流插入数据报。作为重放攻击的一部分,Trudy 发送 R1→R2 的某数据报副本。R2 会否解密并转发该副本?若否,请详细描述 R2 如何检测出副本。
P24. 考虑以下伪 WEP 协议。密钥为 4 位,IV 为 2 位。生成密钥流时将 IV 加至密钥后。假设共享密钥为 1010。四种输入对应的密钥流如下:
101000: 0010101101010101001011010100100 …
101001: 1010011011001010110100100101101 …
101010: 0001101000111100010100101001111 …
101011: 1111101010000000101010100010111 …
所有消息均为 8 位,ICV 为 4 位,为数据前 4 位和后 4 位异或而得。伪 WEP 包含三字段:IV、消息、ICV,其中部分字段被加密。
要使用 IV=11 发送消息 m=10100000,对应三个字段的值是多少?
证明接收方解密后能恢复消息和 ICV。
若 Trudy 拦截一个 WEP 包(IV 不一定为 11)并想篡改转发,设其翻转第一个 ICV 位。在不知道密钥流的前提下,她还需翻转哪些比特才能通过 ICV 检查?
通过修改 (a) 中的 WEP 包比特,解密后验证完整性检查以支持答案。
P25. 提供一个状态防火墙的过滤表和连接表,满足以下限制最强但能满足:
允许所有内部用户发起外部 Telnet 会话;
允许外部用户访问公司网站 222.22.0.12;
阻止其他所有入站和出站流量。
内部网络为 222.22/16。连接表当前缓存三个内部→外部连接,需自行设定合适 IP 地址和端口。
P26. 假设 Alice 想通过类 TOR 服务访问 activist.com。服务使用两个不串通的代理服务器 Proxy1 和 Proxy2。Alice 先从中央服务器获取两个代理的证书(含公钥)。记 RSA 加密解密为 K1+(), K2+(), K1−(), K2−()。
使用时序图提供一简单协议,使 Alice 与 Proxy1 建立共享密钥 S1。记 S1(m) 为密钥 S1 加密/解密数据 m。
使用时序图提供一简单协议,使 Alice 与 Proxy2 建立共享密钥 S2,且 Proxy2 不知 Alice 的 IP。
假设已建立 S1 和 S2。使用时序图提供一简单协议(不使用公钥加密),使 Alice 请求 activist.com 的页面,Proxy2 不知其 IP,Proxy1 不知访问的网站。图最终应以 HTTP 请求到达 activist.com 结束。
P1. Using the monoalphabetic cipher in Figure 8.3 , encode the message “This is an easy problem.” Decode the message “rmij’u uamu xyj.”
P2. Show that Trudy’s known-plaintext attack, in which she knows the (ciphertext, plaintext) translation pairs for seven letters, reduces the number of possible substitutions to be checked in the example in Section 8.2.1 by approximately 109.
P3. Consider the polyalphabetic system shown in Figure 8.4 . Will a chosen-plaintext attack that is able to get the plaintext encoding of the message “The quick brown fox jumps over the lazy dog.” be sufficient to decode all messages? Why or why not?
P4. Consider the block cipher in Figure 8.5 . Suppose that each block cipher Ti simply reverses the order of the eight input bits (so that, for example, 11110000 becomes 00001111). Further suppose that the 64-bit scrambler does not modify any bits (so that the output value of the mth bit is equal to the input value of the mth bit). (a) With n=3 and the original 64-bit input equal to 10100000 repeated eight times, what is the value of the output? (b) Repeat part (a) but now change the last bit of the original 64-bit input from a 0 to a 1. (c) Repeat parts (a) and (b) but now suppose that the 64-bit scrambler inverses the order of the 64 bits.
P5. Consider the block cipher in Figure 8.5 . For a given “key” Alice and Bob would need to keep eight tables, each 8 bits by 8 bits. For Alice (or Bob) to store all eight tables, how many bits of storage are necessary? How does this number compare with the number of bits required for a full-table 64-bit block cipher?
P6. Consider the 3-bit block cipher in Table 8.1 . Suppose the plaintext is 100100100. (a) Initially assume that CBC is not used. What is the resulting ciphertext? (b) Suppose Trudy sniffs the ciphertext. Assuming she knows that a 3-bit block cipher without CBC is being employed (but doesn’t know the specific cipher), what can she surmise? (c) Now suppose that CBC is used with IV=111. What is the resulting ciphertext?
P7. (a) Using RSA, choose p=3 and q=11, and encode the word “dog” by encrypting each letter separately. Apply the decryption algorithm to the encrypted version to recover the original plaintext message. (b) Repeat part (a) but now encrypt “dog” as one message m. P8. Consider RSA with p=5 and q=11.
What are n and z?
Let e be 3. Why is this an acceptable choice for e?
Find d such that de=1 (mod z) and d<160.
Encrypt the message m=8 using the key (n, e). Let c denote the corresponding ciphertext. Show all work. Hint: To simplify the calculations, use the fact: [ (a mod n)⋅(b mod n)]mod n=(a⋅b)modn
P9. In this problem, we explore the Diffie-Hellman (DH) public-key encryption algorithm, which allows two entities to agree on a shared key. The DH algorithm makes use of a large prime number p and another large number g less than p. Both p and g are made public (so that an attacker would know them). In DH, Alice and Bob each independently choose secret keys, SA and SB, respectively. Alice then computes her public key, TA, by raising g to SA and then taking mod p. Bob similarly computes his own public key TB by raising g to SB and then taking mod p. Alice and Bob then exchange their public keys over the Internet. Alice then calculates the shared secret key S by raising TB to SA and then taking mod p. Similarly, Bob calculates the shared key S′ by raising TA to SB and then taking mod p.
Prove that, in general, Alice and Bob obtain the same symmetric key, that is, prove S=S′.
With p = 11 and g = 2, suppose Alice and Bob choose private keys SA=5 and SB=12, respectively. Calculate Alice’s and Bob’s public keys, TA and TB. Show all work.
Following up on part (b), now calculate S as the shared symmetric key. Show all work.
Provide a timing diagram that shows how Diffie-Hellman can be attacked by a man-in- the-middle. The timing diagram should have three vertical lines, one for Alice, one for Bob, and one for the attacker Trudy.
P10. Suppose Alice wants to communicate with Bob using symmetric key cryptography using a session key \(K_S\) . In Section 8.2 , we learned how public-key cryptography can be used to distribute the session key from Alice to Bob. In this problem, we explore how the session key can be distributed—without public key cryptography—using a key distribution center (KDC). The KDC is a server that shares a unique secret symmetric key with each registered user. For Alice and Bob, denote these keys by \(K_{A-KDC}\) and \(K_{B-KDC}\) . Design a scheme that uses the KDC to distribute \(K_S\) to Alice and Bob. Your scheme should use three messages to distribute the session key: a message from Alice to the KDC; a message from the KDC to Alice; and finally a message from Alice to Bob. The first message is \(K_{A-KDC}\) (A, B). Using the notation, \(K_{A-KDC}\), \(K_{B-KDC}\), S, A, and B answer the following questions.
What is the second message?
What is the third message?
P11. Compute a third message, different from the two messages in Figure 8.8 , that has the same checksum as the messages in Figure 8.8 .
P12. Suppose Alice and Bob share two secret keys: an authentication key S1 and a symmetric encryption key S2. Augment Figure 8.9 so that both integrity and confidentiality are provided.
P13. In the BitTorrent P2P file distribution protocol (see Chapter 2 ), the seed breaks the file into blocks, and the peers redistribute the blocks to each other. Without any protection, an attacker can easily wreak havoc in a torrent by masquerading as a benevolent peer and sending bogus blocks to a small subset of peers in the torrent. These unsuspecting peers then redistribute the bogus blocks to other peers, which in turn redistribute the bogus blocks to even more peers. Thus, it is critical for BitTorrent to have a mechanism that allows a peer to verify the integrity of a block, so that it doesn’t redistribute bogus blocks. Assume that when a peer joins a torrent, it initially gets a .torrent file from a fully trusted source. Describe a simple scheme that allows peers to verify the integrity of blocks.
P14. The OSPF routing protocol uses a MAC rather than digital signatures to provide message integrity. Why do you think a MAC was chosen over digital signatures?
P15. Consider our authentication protocol in Figure 8.18 in which Alice authenticates herself to Bob, which we saw works well (i.e., we found no flaws in it). Now suppose that while Alice is authenticating herself to Bob, Bob must authenticate himself to Alice. Give a scenario by which Trudy, pretending to be Alice, can now authenticate herself to Bob as Alice. (Hint: Consider that the sequence of operations of the protocol, one with Trudy initiating and one with Bob initiating, can be arbitrarily interleaved. Pay particular attention to the fact that both Bob and Alice will use a nonce, and that if care is not taken, the same nonce can be used maliciously.)
P16. A natural question is whether we can use a nonce and public key cryptography to solve the end-point authentication problem in Section 8.4 . Consider the following natural protocol: (1) Alice sends the message “I am Alice” to Bob. (2) Bob chooses a nonce, R, and sends it to Alice. (3) Alice uses her private key to encrypt the nonce and sends the resulting value to Bob. (4) Bob applies Alice’s public key to the received message. Thus, Bob computes R and authenticates Alice.
Diagram this protocol, using the notation for public and private keys employed in the textbook.
Suppose that certificates are not used. Describe how Trudy can become a “woman-in- the-middle” by intercepting Alice’s messages and then pretending to be Alice to Bob.
P17. Figure 8.19 shows the operations that Alice must perform with PGP to provide confidentiality, authentication, and integrity. Diagram the corresponding operations that Bob must perform on the package received from Alice.
P18. Suppose Alice wants to send an e-mail to Bob. Bob has a public-private key pair (KB+,KB−), and Alice has Bob’s certificate. But Alice does not have a public, private key pair. Alice and Bob (and the entire world) share the same hash function H(⋅).
In this situation, is it possible to design a scheme so that Bob can verify that Alice created the message? If so, show how with a block diagram for Alice and Bob.
Is it possible to design a scheme that provides confidentiality for sending the message from Alice to Bob? If so, show how with a block diagram for Alice and Bob.
P19. Consider the Wireshark output below for a portion of an SSL session.
Is Wireshark packet 112 sent by the client or server?
What is the server’s IP address and port number?
Assuming no loss and no retransmissions, what will be the sequence number of the next TCP segment sent by the client?
How many SSL records does Wireshark packet 112 contain?
Does packet 112 contain a Master Secret or an Encrypted Master Secret or neither?
Assuming that the handshake type field is 1 byte and each length field is 3 bytes, what are the values of the first and last bytes of the Master Secret (or Encrypted Master Secret)?
The client encrypted handshake message takes into account how many SSL records?
The server encrypted handshake message takes into account how many SSL records?
P20. In Section 8.6.1 , it is shown that without sequence numbers, Trudy (a woman-in-the middle) can wreak havoc in an SSL session by interchanging TCP segments. Can Trudy do something similar by deleting a TCP segment? What does she need to do to succeed at the deletion attack? What effect will it have?

(Wireshark screenshot reprinted by permission of the Wireshark Foundation.)
P21. Suppose Alice and Bob are communicating over an SSL session. Suppose an attacker, who does not have any of the shared keys, inserts a bogus TCP segment into a packet stream with correct TCP checksum and sequence numbers (and correct IP addresses and port numbers). Will SSL at the receiving side accept the bogus packet and pass the payload to the receiving application? Why or why not?
P22. The following true/false questions pertain to Figure 8.28 .
When a host in 172.16.1/24 sends a datagram to an Amazon.com server, the router R1 will encrypt the datagram using IPsec.
When a host in 172.16.1/24 sends a datagram to a host in 172.16.2/24, the router R1 will change the source and destination address of the IP datagram.
Suppose a host in 172.16.1/24 initiates a TCP connection to a Web server in 172.16.2/24. As part of this connection, all datagrams sent by R1 will have protocol number 50 in the left-most IPv4 header field.
Consider sending a TCP segment from a host in 172.16.1/24 to a host in 172.16.2/24. Suppose the acknowledgment for this segment gets lost, so that TCP resends the segment. Because IPsec uses sequence numbers, R1 will not resend the TCP segment.
P23. Consider the example in Figure 8.28 . Suppose Trudy is a woman-in-the-middle, who can insert datagrams into the stream of datagrams going from R1 and R2. As part of a replay attack, Trudy sends a duplicate copy of one of the datagrams sent from R1 to R2. Will R2 decrypt the duplicate datagram and forward it into the branch-office network? If not, describe in detail how R2 detects the duplicate datagram.
P24. Consider the following pseudo-WEP protocol. The key is 4 bits and the IV is 2 bits. The IV is appended to the end of the key when generating the keystream. Suppose that the shared secret key is 1010. The keystreams for the four possible inputs are as follows:
101000: 0010101101010101001011010100100 …
101001: 1010011011001010110100100101101 …
101010: 0001101000111100010100101001111 …
101011: 1111101010000000101010100010111 …
Suppose all messages are 8 bits long. Suppose the ICV (integrity check) is 4 bits long, and is calculated by XOR-ing the first 4 bits of data with the last 4 bits of data. Suppose the pseudo- WEP packet consists of three fields: first the IV field, then the message field, and last the ICV field, with some of these fields encrypted.
We want to send the message m=10100000 using the IV=11 and using WEP. What will be the values in the three WEP fields?
Show that when the receiver decrypts the WEP packet, it recovers the message and the ICV.
Suppose Trudy intercepts a WEP packet (not necessarily with the IV=11) and wants to modify it before forwarding it to the receiver. Suppose Trudy flips the first ICV bit. Assuming that Trudy does not know the keystreams for any of the IVs, what other bit(s) must Trudy also flip so that the received packet passes the ICV check?
Justify your answer by modifying the bits in the WEP packet in part (a), decrypting the resulting packet, and verifying the integrity check.
P25. Provide a filter table and a connection table for a stateful firewall that is as restrictive as possible but accomplishes the following:
Allows all internal users to establish Telnet sessions with external hosts.
Allows external users to surf the company Web site at 222.22.0.12.
But otherwise blocks all inbound and outbound traffic.
The internal network is 222.22/16. In your solution, suppose that the connection table is currently caching three connections, all from inside to outside. You’ll need to invent appropriate IP addresses and port numbers.
P26. Suppose Alice wants to visit the Web site activist.com using a TOR-like service. This service uses two non-colluding proxy servers, Proxy1 and Proxy2. Alice first obtains the certificates (each containing a public key) for Proxy1 and Proxy2 from some central server. Denote K1+(),K2+(),K1−(), and K2−() for the encryption/decryption with public and private RSA keys.
Using a timing diagram, provide a protocol (as simple as possible) that enables Alice to establish a shared session key S1 with Proxy1. Denote S1(m) for encryption/decryption of data m with the shared key S1.
Using a timing diagram, provide a protocol (as simple as possible) that allows Alice to establish a shared session key S2 with Proxy2 without revealing her IP address to Proxy2.
Assume now that shared keys S1 and S2 are now established. Using a timing diagram, provide a protocol (as simple as possible and not using public-key cryptography) that allows Alice to request an html page from activist.com without revealing her IP address to Proxy2 and without revealing to Proxy1 which site she is visiting. Your diagram should end with an HTTP request arriving at activist.com.