8.2 密码学原理

8.2 Principles of Cryptography

尽管密码学的历史可以追溯到至少凯撒大帝时代，但现代密码技术（包括许多用于互联网的技术）是基于过去三十年取得的进展。Kahn 的著作《The Codebreakers》 [Kahn 1967] 和 Singh 的《The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography》 [Singh 1999] 提供了对密码学悠久历史的精彩回顾。要全面讨论密码学本身需要一本完整的书 [Kaufman 1995; Schneier 1995]，因此我们这里只涉及密码学的基本方面，特别是它在互联网上的实际应用。我们还指出，尽管本节的重点是密码学在保密性方面的应用，但很快我们将看到密码技术也与身份验证、消息完整性、不可否认性等密不可分。

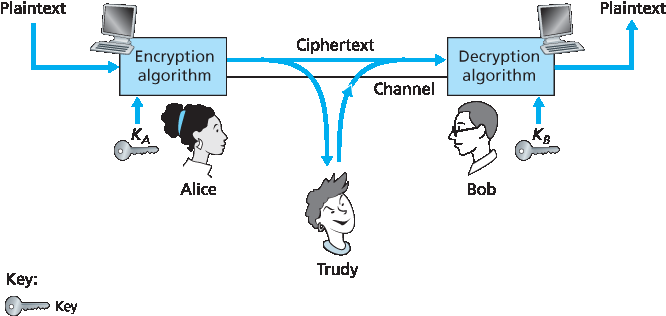
图 8.2 密码学组成部分

密码技术允许发送方对数据进行伪装，使得入侵者无法从被截获的数据中获取任何信息。当然，接收方必须能够从伪装后的数据中恢复原始数据。图 8.2 展示了一些重要术语。

现在假设 Alice 想向 Bob 发送一条消息。Alice 的消息以原始形式存在（例如，“Bob，我爱你。Alice”），称为 明文（plaintext） 或 清文（cleartext）。Alice 使用一种 加密算法（encryption algorithm） 对她的明文消息进行加密，使得加密后的消息（称为 密文（ciphertext））对于任何入侵者来说都是不可读的。有趣的是，在许多现代密码系统中，包括那些在互联网上使用的系统，加密技术本身是公开的——发布、标准化并对所有人开放（例如 [RFC 1321; RFC 3447; RFC 2420; NIST 2001]），甚至包括潜在的入侵者！显然，如果每个人都知道数据的编码方法，那么一定存在某些秘密信息可以防止入侵者解密传输的数据。这正是 密钥（key） 发挥作用的地方。

在 图 8.2 中，Alice 提供了一个密钥 KA，这是一串数字或字符，作为加密算法的输入。加密算法以密钥和明文消息 m 为输入，输出密文。记号 KA(m) 表示使用密钥 KA 加密后的明文消息 m 的密文形式。使用密钥 KA 的实际 加密算法 将由上下文确定。同样，Bob 将提供一个密钥 KB 给 解密算法（decryption algorithm），该算法以密文和 Bob 的密钥为输入，输出原始明文。也就是说，如果 Bob 收到一条加密消息 KA(m)，他通过计算 KB(KA(m)) = m 来解密。

在 对称密钥系统（symmetric key systems） 中，Alice 和 Bob 的密钥是相同的，并且是保密的。而在 公钥系统（public key systems） 中，使用一对密钥。其中一个密钥对 Bob 和 Alice 都是已知的（实际上是向全世界公开的）。另一个密钥仅为 Bob 或 Alice 所知（但不是两者）。在接下来的两个小节中，我们将更详细地探讨对称密钥系统和公钥系统。

Although cryptography has a long history dating back at least as far as Julius Caesar, modern cryptographic techniques, including many of those used in the Internet, are based on advances made in the past 30 years. Kahn’s book, The Codebreakers [Kahn 1967], and Singh’s book, The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography [Singh 1999], provide a fascinating look at the long history of cryptography. A complete discussion of cryptography itself requires a complete book [Kaufman 1995; Schneier 1995] and so we only touch on the essential aspects of cryptography, particularly as they are practiced on the Internet. We also note that while our focus in this section will be on the use of cryptography for confidentiality, we’ll see shortly that cryptographic techniques are inextricably woven into authentication, message integrity, nonrepudiation, and more.

Figure 8.2 Cryptographic components

Cryptographic techniques allow a sender to disguise data so that an intruder can gain no information from the intercepted data. The receiver, of course, must be able to recover the original data from the disguised data. Figure 8.2 illustrates some of the important terminology.

Suppose now that Alice wants to send a message to Bob. Alice’s message in its original form (for example, “Bob, I love you. Alice”) is known as p­ laintext, or cleartext. Alice encrypts her plaintext message using an encryption algorithm so that the encrypted message, known as ciphertext, looks unintelligible to any intruder. Interestingly, in many modern cryptographic systems, including those used in the Internet, the encryption technique itself is known—published, standardized, and available to everyone (for example, [RFC 1321; RFC 3447; RFC 2420; NIST 2001]), even a potential intruder! Clearly, if everyone knows the method for encoding data, then there must be some secret information that prevents an intruder from decrypting the transmitted data. This is where keys come in.

In Figure 8.2, Alice provides a key, KA, a string of numbers or characters, as input to the encryption algorithm. The encryption algorithm takes the key and the plaintext message, m, as input and produces ciphertext as output. The notation KA(m) refers to the ciphertext form (encrypted using the key KA) of the plaintext message, m. The actual encryption algorithm that uses key KA will be evident from the context. Similarly, Bob will provide a key, KB, to the decryption algorithm that takes the ciphertext and Bob’s key as input and produces the original plaintext as output. That is, if Bob receives an encrypted message KA(m), he decrypts it by computing KB(KA(m))=m. In symmetric key systems, Alice’s and Bob’s keys are identical and are secret. In public key systems, a pair of keys is used. One of the keys is known to both Bob and Alice (indeed, it is known to the whole world). The other key is known only by either Bob or Alice (but not both). In the following two subsections, we consider symmetric key and public key systems in more detail.

8.2.1 对称密钥密码学

8.2.1 Symmetric Key Cryptography

所有的密码算法都涉及将一种东西替换为另一种，例如将一段明文转换并替换为相应的密文以创建加密消息。在学习现代基于密钥的密码系统之前，我们先通过研究一种非常古老、非常简单的对称密钥算法来入门，这种算法归功于尤利乌斯·凯撒，称为 凯撒密码（Caesar cipher） （cipher 是加密数据的方法）。

对于英文文本，凯撒密码通过将明文消息中的每个字母替换为字母表中向后数第 k 个字母（允许环绕，即 z 后面是 a）来实现加密。例如，如果 k=3，那么明文中的字母 a 在密文中变为 d； b 变为 e，依此类推。此处， k 的值即为密钥。例如，明文消息 “bob, i love you. Alice” 在密文中变为 “ere, l oryh brx. dolfh”。虽然密文看起来确实像乱码，但如果知道使用了凯撒密码，那么破解这个代码不会花太久时间，因为只存在 25 种可能的密钥值。

凯撒密码的一种改进是 单表代换密码（monoalphabetic cipher），它同样用另一个字母替代字母表中的一个字母。然而，它不是使用固定的偏移模式（例如所有字母偏移 k 位）来替换，而是任意字母都可以替换为另一个字母，只要每个字母有唯一的替代字母，且彼此之间是唯一对应的。图 8.3 中的替换规则展示了一种可能的明文编码规则。

明文消息 “bob, i love you. Alice” 变为 “nkn, s gktc wky. Mgsbc.” 因此，与凯撒密码一样，这看起来像乱码。单表代换密码看起来比凯撒密码更安全，因为它存在 ``26!``（约等于 10 的 26 次方）种字母配对方式，而非仅有的 25 种。但用穷举法尝试所有 \(10^26\) 种配对

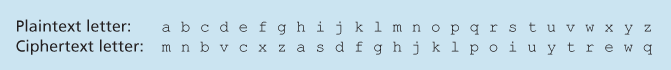
图 8.3 单表代换密码

需要的工作量太大，不可能成为破解算法和解码消息的可行方式。然而，通过对明文语言的统计分析，例如知道英文字母 e 和 t 是最常出现的字母（分别占字母出现频率的 13% 和 9%），并知道某些二字母或三字母组合经常一起出现（如 “in”、“it”、“the”、“ion”、“ing” 等），就能相对容易地破解这种代码。如果入侵者对消息内容有所了解，那么破解就更容易了。例如，如果入侵者 Trudy 是 Bob 的妻子，并怀疑 Bob 与 Alice 有染，那么她可能会怀疑消息中出现了 “bob” 和 “alice”。如果 Trudy 确定这两个名字出现在密文中，并拿到上面的密文实例，她就可以立即确定 26 个字母配对中的 7 个，从而使穷举法减少 \(10^9\) 种组合。事实上，如果 Trudy 怀疑 Bob 有外遇，她很可能还会在消息中寻找其他敏感词。

在考虑 Trudy 破解 Bob 与 Alice 加密方案的难易程度时，可以根据入侵者掌握的信息区分三种不同的攻击场景：

• 仅密文攻击（Ciphertext-only attack）。在某些情况下，入侵者只能访问截获的密文，而对明文内容毫无把握。我们已经看到统计分析如何在 仅密文攻击 中帮助破解加密方案。

• 已知明文攻击（Known-plaintext attack）。我们在上面看到，如果 Trudy 知道 “bob” 和 “alice” 出现在密文中，那么她就可以确定字母 a、l、i、c、e、b 和 o 的（明文，密文）配对。Trudy 还可能运气好地记录了所有密文传输内容，并在某张纸上找到了 Bob 写下的一次解密版本。当入侵者已知一些（明文，密文）配对时，我们称这种攻击为 已知明文攻击。

• 选择明文攻击（Chosen-plaintext attack）。在 选择明文攻击 中，入侵者能够选择明文消息，并获得其对应的密文形式。对于我们目前看到的这些简单加密算法来说，如果 Trudy 能让 Alice 发送消息 “The quick brown fox jumps over the lazy dog”，她就能完全破解该加密方案。我们很快会看到，对于更复杂的加密技术，选择明文攻击并不一定意味着该加密技术能够被破解。

大约五百年前，出现了一种对单表代换加密进行改进的技术，称为 多表代换加密（polyalphabetic encryption）。多表加密的思想是使用多个单表代换密码，并针对明文消息中某个特定位置的字母使用特定的单表代换密码进行编码。因此，相同的字母在明文消息中出现在不同位置时，其编码可能不同。图 8.4 展示了一个多表加密方案的例子。它使用了两个凯撒密码（ k=5 和 k=19），分别显示为两行。我们可以选择按重复模式 C1、 C2、 C2、 C1、C2 使用这两个凯撒密码 C1 和 C2。即，第一位明文字母使用 C1 编码，第二和第三位使用 C2，第四位使用 C1，第五位使用 C2，接下来重复此模式，第六位使用 C1，第七位使用 C2，以此类推。明文消息 “bob, i love you.” 加密后变为 “ghu, n etox dhz.” 注意，明文中第一个 b 使用 C1 加密，而第二个 b 使用 C2 加密。在本例中，加密和解密的“密钥”就是两个凯撒密钥（ k=5， k=19）和模式 C1、 C2、 C2、 C1、 C2 的知识。

All cryptographic algorithms involve substituting one thing for another, for example, taking a piece of plaintext and then computing and substituting the appropriate ciphertext to create the encrypted message. Before studying a modern key-based cryptographic system, let us first get our feet wet by studying a very old, very simple symmetric key algorithm attributed to Julius Caesar, known as the Caesar cipher (a cipher is a method for encrypting data).

For English text, the Caesar cipher would work by taking each letter in the plaintext message and substituting the letter that is k letters later (allowing wraparound; that is, having the letter z followed by the letter a) in the alphabet. For example if k=3, then the letter a in plaintext becomes d in ciphertext; b in plaintext becomes e in ciphertext, and so on. Here, the value of k serves as the key. As an example, the plaintext message “bob, i love you. Alice” becomes “ere, l oryh brx. dolfh” in ciphertext. While the ciphertext does indeed look like gibberish, it wouldn’t take long to break the code if you knew that the Caesar cipher was being used, as there are only 25 possible key values.

An improvement on the Caesar cipher is the monoalphabetic cipher, which also substitutes one letter of the alphabet with another letter of the alphabet. ­However, rather than substituting according to a regular pattern (for example, substitution with an offset of k for all letters), any letter can be substituted for any other letter, as long as each letter has a unique substitute letter, and vice versa. The substitution rule in Figure 8.3 shows one possible rule for encoding plaintext.

The plaintext message “bob, i love you. Alice” becomes “nkn, s gktc wky. Mgsbc.” Thus, as in the case of the Caesar cipher, this looks like gibberish. A monoalphabetic cipher would also appear to be better than the Caesar cipher in that there are 26! (on the order of 1026) possible pairings of letters rather than 25 possible pairings. A brute-force approach of trying all 1026 possible pairings

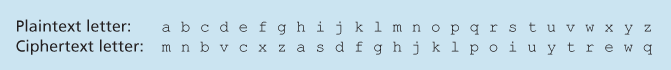
Figure 8.3 A monoalphabetic cipher

would require far too much work to be a feasible way of breaking the encryption algorithm and decoding the message. However, by statistical analysis of the plaintext language, for example, knowing that the letters e and t are the most frequently occurring letters in typical English text (accounting for 13 percent and 9 percent of letter occurrences), and knowing that particular two-and three-letter occurrences of letters appear quite often together (for example, “in,” “it,” “the,” “ion,” “ing,” and so forth) make it relatively easy to break this code. If the intruder has some knowledge about the possible contents of the message, then it is even easier to break the code. For example, if Trudy the intruder is Bob’s wife and suspects Bob of having an affair with Alice, then she might suspect that the names “bob” and “alice” appear in the text. If Trudy knew for certain that those two names appeared in the ciphertext and had a copy of the example ciphertext message above, then she could immediately determine seven of the 26 letter pairings, requiring 109 fewer possibilities to be checked by a brute-force method. Indeed, if Trudy suspected Bob of having an affair, she might well expect to find some other choice words in the message as well.

When considering how easy it might be for Trudy to break Bob and Alice’s encryption scheme, one can distinguish three different scenarios, depending on what information the intruder has.

• Ciphertext-only attack. In some cases, the intruder may have access only to the intercepted ciphertext, with no certain information about the contents of the plaintext message. We have seen how statistical analysis can help in a ciphertext-only attack on an encryption scheme.

• Known-plaintext attack. We saw above that if Trudy somehow knew for sure that “bob” and “alice” appeared in the ciphertext message, then she could have determined the (plaintext, ciphertext) pairings for the letters a, l, i, c, e, b, and o. Trudy might also have been fortunate enough to have recorded all of the ciphertext transmissions and then found Bob’s own decrypted version of one of the transmissions scribbled on a piece of paper. When an intruder knows some of the (plaintext, ciphertext) pairings, we refer to this as a known-plaintext attack on the encryption scheme.

• Chosen-plaintext attack. In a chosen-plaintext attack, the intruder is able to choose the plaintext message and obtain its corresponding ciphertext form. For the simple encryption algorithms we’ve seen so far, if Trudy could get Alice to send the message, “The quick brown fox jumps over the lazy dog,” she could completely break the encryption scheme. We’ll see shortly that for more sophisticated encryption techniques, a chosen-plaintext attack does not necessarily mean that the encryption technique can be broken.

Five hundred years ago, techniques improving on monoalphabetic encryption, known as polyalphabetic encryption, were invented. The idea behind polyalphabetic encryption is to use multiple monoalphabetic ciphers, with a specific

Figure 8.4 A monoalphabetic cipher

monoalphabetic cipher to encode a letter in a specific position in the plaintext message. Thus, the same letter, appearing in different positions in the plaintext message, might be encoded differently. An example of a polyalphabetic encryption scheme is shown in Figure 8.4. It has two Caesar ciphers (with k=5 and k=19), shown as rows. We might choose to use these two Caesar ciphers, C1 and C2, in the repeating pattern C1, C2, C2, C1, C2. That is, the first letter of plaintext is to be encoded using C1, the second and third using C2, the fourth using C1, and the fifth using C2. The pattern then repeats, with the sixth letter being encoded using C1, the seventh with C2, and so on. The plaintext message “bob, i love you.” is thus encrypted “ghu, n etox dhz.” Note that the first b in the plaintext message is encrypted using C1, while the second b is encrypted using C2. In this example, the encryption and decryption “key” is the knowledge of the two Caesar keys (k=5, k=19) and the pattern C1, C2, C2, C1, C2.

块加密

Block Ciphers

现在我们进入现代，看看当前对称密钥加密是如何进行的。对称加密技术大致可分为两类： 流密码（stream ciphers） 和 块密码（block ciphers）。我们将在 第 8.7 节 简要介绍流密码，在研究无线局域网的安全性时使用它们。本节我们专注于块密码，它被用于许多安全的 Internet 协议中，包括 PGP（用于安全电子邮件）、SSL（用于保护 TCP 连接）和 IPsec（用于保护网络层传输）。

在块密码中，要加密的消息以 k 位为单位的块进行处理。例如，如果 k=64，则消息被划分为若干 64 位块，每个块被单独加密。为了对一个块编码，密码算法使用一对一映射将 k 位明文块映射到 k 位密文块。我们来看一个例子。假设 k=3，则该块密码将 3 位输入（明文）映射为 3 位输出（密文）。表 8.1 给出了一个可能的映射。请注意，这是一种一对一映射；即每个输入都有不同的输出。该块密码将消息分解为 3 位块，并根据上述映射加密每个块。你应该验证消息 010110001111 被加密为 101000111001。

继续这个 3 位块的例子，注意 表 8.1 中的映射只是众多可能映射中的一种。那么，有多少种可能的映射呢？为了回答这个问题，观察到映射不过是所有可能输入的排列。共有 2^3(=8) 个可能输入（列于输入列下方）。这八个输入可以以 8! = 40,320 种不同方式排列。由于每种排列定义一个映射，因此存在 40,320 个可能的映射。我们可以将每个映射看作一个密钥——如果 Alice 和 Bob 都知道该映射（即密钥），他们就能对彼此间发送的消息进行加密和解密。

表 8.1 一个具体的 3 位块密码

输入	输出	输入	输出
000	110	100	011
001	111	101	010
010	101	110	000
011	100	111	001

这种密码的暴力破解方法是尝试所有映射来解密密文。仅有 40,320 个映射（当 k=3）时，可以在一台台式机上快速完成。为防止暴力攻击，块密码通常使用更大的块，例如 k=64 位或更大。注意，一般 k 块密码的可能映射数量是 2^k!，即使是中等大小的 k`（如 ``k=64`），其值也大得惊人。

虽然上述具有中等 k 值的全表块密码可以提供强大的对称密钥加密方案，但它们不易实现。对于 k=64 和某个给定映射，Alice 和 Bob 需要维护一个包含 2^64 个输入值的表，这是不可行的任务。而且，如果 Alice 和 Bob 改变密钥，他们必须重新生成该表。因此，提供所有输入和输出之间预定义映射的全表块密码（如上例）是不现实的。

相反，块密码通常使用函数来模拟随机排列的表。图 8.5 展示了一个这种函数的例子（改编自 [Kaufman 1995]），用于 k=64 位。该函数首先将一个 64 位块分解为 8 个 8 位小块。每个 8 位小块通过一个 8 位到 8 位的表处理，该表尺寸是可管理的。例如，第一个小块由表 T1 处理。然后，将这 8 个输出小块重新组装为一个 64 位块。接着对该块中的 64 位进行扰乱（排列），以生成一个 64 位输出。该输出再反馈到 64 位输入中，开始另一个循环。经过 n 次循环后，该函数生成一个 64 位的密文块。多个轮次的目的是让每个输入位影响大多数（甚至全部）输出位。（如果仅使用一轮，某个输入位只会影响 64 个输出位中的 8 个。）此块密码算法的密钥为这八个置换表（假设扰乱函数是公开的）。

图 8.5 块密码示例

目前存在多个流行的块密码标准，包括 DES（数据加密标准）、3DES 和 AES（高级加密标准）。这些标准都使用类似于 图 8.5 中的函数（虽然更复杂、且每种密码具体不同），而不是预定义的表。它们也都使用一串比特作为密钥。例如，DES 使用 64 位块和 56 位密钥。AES 使用 128 位块，密钥长度可以是 128、 192 或 256 位。一个算法的密钥决定了算法内部“微型表”的映射和置换。破解这些密码的暴力攻击方法是遍历所有可能的密钥，并使用每个密钥运行解密算法。注意，密钥长度为 n 时，存在 2^n 个可能密钥。 NIST [NIST 2001] 估算：一台能在 1 秒内破解 56 位 DES（即尝试所有 2^56 个密钥）的机器，破解一个 128 位 AES 密钥大约需要 149 万亿年。

Let us now move forward to modern times and examine how symmetric key encryption is done today. There are two broad classes of symmetric encryption techniques: stream ciphers and block ciphers. We’ll briefly examine stream ciphers in ­Section 8.7 when we investigate security for wireless LANs. In this section, we focus on block ciphers, which are used in many secure Internet protocols, including PGP (for secure e-mail), SSL (for securing TCP connections), and IPsec (for securing the network-layer transport).

In a block cipher, the message to be encrypted is processed in blocks of k bits. For example, if k=64, then the message is broken into 64-bit blocks, and each block is encrypted independently. To encode a block, the cipher uses a one-to-one mapping to map the k-bit block of cleartext to a k-bit block of ciphertext. Let’s look at an example. Suppose that k=3, so that the block cipher maps 3-bit inputs (cleartext) to 3-bit outputs (ciphertext). One possible mapping is given in Table 8.1. Notice that this is a one-to-one mapping; that is, there is a different output for each input. This block cipher breaks the message up into 3-bit blocks and encrypts each block according to the above mapping. You should verify that the message 010110001111 gets encrypted into 101000111001.

Continuing with this 3-bit block example, note that the mapping in Table 8.1 is just one mapping of many possible mappings. How many possible mappings are there? To answer this question, observe that a mapping is nothing more than a permutation of all the possible inputs. There are 23(=8) possible inputs (listed under the input columns). These eight inputs can be permuted in 8!=40,320 different ways. Since each of these permutations specifies a mapping, there are 40,320 possible mappings. We can view each of these mappings as a key—if Alice and Bob both know the mapping (the key), they can encrypt and decrypt the messages sent between them.

Table 8.1 A specific 3-bit block cipher

input	output	input	output
000	110	100	011
001	111	101	010
010	101	110	000
011	100	111	001

The brute-force attack for this cipher is to try to decrypt ciphtertext by using all mappings. With only 40,320 mappings (when k=3), this can quickly be accomplished on a desktop PC. To thwart brute-force attacks, block ciphers typically use much larger blocks, consisting of k=64 bits or even larger. Note that the number of possible mappings for a general k-block cipher is 2k!, which is astronomical for even moderate values of k (such as k=64).

Although full-table block ciphers, as just described, with moderate values of k can produce robust symmetric key encryption schemes, they are unfortunately difficult to implement. For k=64 and for a given mapping, Alice and Bob would need to maintain a table with 264 input values, which is an infeasible task. Moreover, if Alice and Bob were to change keys, they would have to each regenerate the table. Thus, a full-table block cipher, providing predetermined mappings between all inputs and outputs (as in the example above), is simply out of the question.

Instead, block ciphers typically use functions that simulate randomly permuted tables. An example (adapted from [Kaufman 1995]) of such a function for k=64 bits is shown in Figure 8.5. The function first breaks a 64-bit block into 8 chunks, with each chunk consisting of 8 bits. Each 8-bit chunk is processed by an 8-bit to 8-bit table, which is of manageable size. For example, the first chunk is processed by the table denoted by T1. Next, the 8 output chunks are reassembled into a 64-bit block. The positions of the 64 bits in the block are then scrambled (permuted) to produce a 64-bit output. This output is fed back to the 64-bit input, where another cycle begins. After n such cycles, the function provides a 64-bit block of ciphertext. The purpose of the rounds is to make each input bit affect most (if not all) of the final output bits. (If only one round were used, a given input bit would affect only 8 of the 64 output bits.) The key for this block cipher algorithm would be the eight permutation tables (assuming the scramble function is publicly known).

Figure 8.5 An example of a block cipher

Today there are a number of popular block ciphers, including DES (standing for Data Encryption Standard), 3DES, and AES (standing for Advanced Encryption Standard). Each of these standards uses functions, rather than predetermined tables, along the lines of Figure 8.5 (albeit more complicated and specific to each cipher). Each of these algorithms also uses a string of bits for a key. For example, DES uses 64-bit blocks with a 56-bit key. AES uses 128-bit blocks and can operate with keys that are 128, 192, and 256 bits long. An algorithm’s key determines the specific “mini-table” mappings and permutations within the algorithm’s internals. The brute-force attack for each of these ciphers is to cycle through all the keys, applying the decryption algorithm with each key. Observe that with a key length of n, there are 2n possible keys. NIST [NIST 2001] estimates that a machine that could crack 56-bit DES in one second (that is, try all 256 keys in one second) would take approximately 149 trillion years to crack a 128-bit AES key.

密码块链接（CBC）

Cipher-Block Chaining

在计算机网络应用中，我们通常需要加密长消息（或长数据流）。如果我们直接按上述方法将消息分割为 k 位块并独立加密每个块，会出现一个微妙但重要的问题。注意，两个或多个明文块可能是相同的。例如，多个块的明文可能是 “HTTP/1.1”。对于这些相同的块，块密码当然会产生相同的密文。攻击者可能会在看到相同的密文块时猜测明文，并甚至通过识别相同的密文块并利用底层协议结构知识来解密整个消息 [Kaufman 1995]。

为了解决这个问题，我们可以在密文中引入一些随机性，使得相同的明文块生成不同的密文块。为解释这个想法，令 m(i) 表示第 i 个明文块， c(i) 表示第 i 个密文块， a⊕b 表示两个比特串 a 和 b 的异或运算。（回忆： 0⊕0=1⊕1=0， 0⊕1=1⊕0=1，异或按位执行。例如， 10101010⊕11110000=01011010。）还令密钥为 S 的块密码算法记为 KS。基本思想如下。发送方为第 i 个块生成一个随机的 k 位数 r(i)，然后计算 c(i)=KS(m(i)⊕r(i))。注意，每个块使用一个新的 k 位随机数。然后发送方发送 c(1)、r(1)、c(2)、r(2)、c(3)、r(3)，依此类推。由于接收方接收到 c(i) 和 r(i)，它可以通过计算 m(i)=KS(c(i))⊕r(i) 来恢复每个明文块。重要的是，虽然 r(i) 是明文发送的，因此 Trudy 可以监听，但她无法获取明文 m(i)，因为她不知道密钥 KS。此外，若两个明文块 m(i) 和 m(j) 相同，只要 r(i) 和 r(j) 不同（几乎总是如此），对应的密文块 c(i) 和 c(j) 也将不同。

例如，考虑 表 8.1 中的 3 位块密码。假设明文为 010010010。如果 Alice 直接加密而不引入随机性，密文为 101101101。如果 Trudy 监听此密文，由于三个密文块相同，她可以正确猜出三个明文块也相同。现在假设 Alice 生成随机块 r(1)=001、 r(2)=111 和 r(3)=100，并使用上述技术生成密文 c(1)=100、 c(2)=010 和 c(3)=000。注意，尽管明文块相同，但三个密文块不同。然后 Alice 发送 c(1)、r(1)、c(2)、r(2)。你应验证 Bob 可使用共享密钥 KS 恢复原始明文。

敏锐的读者会注意到，引入随机性解决了一个问题却引入了另一个问题：即 Alice 现在必须传输两倍的数据。确实，每个密文比特都必须额外发送一个随机比特，从而带宽需求加倍。为了鱼与熊掌兼得，块密码通常使用一种称为 密码块链接（Cipher Block Chaining，CBC） 的技术。其基本思想是只在第一条消息中发送一个随机值，然后发送方与接收方使用计算出的密文块代替后续的随机数。具体而言，CBC 的操作如下：

1. 在加密消息（或数据流）之前，发送方生成一个随机的 k 位字符串，称为初始化向量（Initialization Vector，IV）。记作 c(0)。发送方以明文形式将 IV 发送给接收方。

2. 对于第一个块，发送方计算 m(1)⊕c(0)，即将明文第一块与 IV 做异或运算。然后将结果输入块加密算法，得到相应的密文块，即 c(1)=KS(m(1)⊕c(0))。发送方将加密后的块 c(1) 发送给接收方。

3. 对于第 i 个块，发送方使用 c(i)=KS(m(i)⊕c(i-1)) 生成第 i 个密文块。

现在让我们来看看这种方法的一些后果。首先，接收方仍然能够恢复原始消息。确实，当接收方收到 c(i) 时，它使用 KS 解密，得到 s(i)=m(i)⊕c(i-1)；由于接收方也知道 c(i-1)，因此可以通过 m(i)=s(i)⊕c(i-1) 得到明文块。其次，即使两个明文块相同，对应的密文块几乎总是不同。第三，虽然发送方以明文发送 IV，入侵者仍然无法解密密文块，因为入侵者不知道密钥 S。最后，发送方只需发送一个附加块（即 IV），因此对于包含数百个块的长消息来说，带宽开销几乎可以忽略不计。

例如，让我们使用 表 8.1 中的 3 位块密码，明文为 010010010， IV=c(0)=001，来确定密文。发送方首先使用 IV 计算 c(1)=KS(m(1)⊕c(0))=100。接着计算 c(2)=KS(m(2)⊕c(1))=KS(010⊕100)=000， c(3)=KS(m(3)⊕c(2))=KS(010⊕000)=101。读者应验证，接收方知道 IV 和 KS 后可以恢复原始明文。

CBC 在设计安全网络协议时具有一个重要含义：我们需要在协议中提供机制，将 IV 从发送方分发给接收方。我们将在本章后续部分看到几种协议是如何实现这一点的。

In computer networking applications, we typically need to encrypt long messages (or long streams of data). If we apply a block cipher as described by simply chopping up the message into k-bit blocks and independently encrypting each block, a subtle but important problem occurs. To see this, observe that two or more of the cleartext blocks can be identical. For example, the cleartext in two or more blocks could be “HTTP/1.1”. For these identical blocks, a block cipher would, of course, produce the same ciphertext. An attacker could potentially guess the cleartext when it sees identical ciphertext blocks and may even be able to decrypt the entire message by identifying identical ciphtertext blocks and using knowledge about the underlying protocol structure [Kaufman 1995].

To address this problem, we can mix some randomness into the ciphertext so that identical plaintext blocks produce different ciphertext blocks. To explain this idea, let m(i) denote the ith plaintext block, c(i) denote the ith ciphertext block, and a⊕b denote the exclusive-or (XOR) of two bit strings, a and b. (Recall that the 0⊕0=1⊕1=0 and 0⊕1=1⊕0=1, and the XOR of two bit strings is done on a bit-by-bit basis. So, for example, 10101010⊕11110000=01011010.) Also, denote the block-cipher encryption algorithm with key S as KS. The basic idea is as follows. The sender creates a random k-bit number r(i) for the ith block and calculates c(i)=KS(m(i)⊕r(i)). Note that a new k-bit random number is chosen for each block. The sender then sends c(1), r(1), c(2), r(2), c(3), r(3), and so on. Since the receiver receives c(i) and r(i), it can recover each block of the plaintext by computing m(i)=KS(c(i))⊕r(i). It is important to note that, although r(i) is sent in the clear and thus can be sniffed by Trudy, she cannot obtain the plaintext m(i), since she does not know the key KS. Also note that if two plaintext blocks m(i) and m(j) are the same, the corresponding ciphertext blocks c(i) and c(j) will be different (as long as the random numbers r(i) and r(j) are different, which occurs with very high probability).

As an example, consider the 3-bit block cipher in Table 8.1. Suppose the plaintext is 010010010. If Alice encrypts this directly, without including the randomness, the resulting ciphertext becomes 101101101. If Trudy sniffs this ciphertext, because each of the three cipher blocks is the same, she can correctly surmise that each of the three plaintext blocks are the same. Now suppose instead Alice generates the random blocks r(1)=001, r(2)=111, and r(3)=100 and uses the above technique to generate the ciphertext c(1)=100, c(2)=010, and c(3)=000. Note that the three ciphertext blocks are different even though the plaintext blocks are the same. Alice then sends c(1), r(1), c(2), and r(2). You should verify that Bob can obtain the original plaintext using the shared key KS.

The astute reader will note that introducing randomness solves one problem but creates another: namely, Alice must transmit twice as many bits as before. Indeed, for each cipher bit, she must now also send a random bit, doubling the required bandwidth. In order to have our cake and eat it too, block ciphers typically use a technique called Cipher Block Chaining (CBC). The basic idea is to send only one random value along with the very first message, and then have the sender and receiver use the computed coded blocks in place of the subsequent random number. Specifically, CBC operates as follows:

1. Before encrypting the message (or the stream of data), the sender generates a random k-bit string, called the Initialization Vector (IV). Denote this initialization vector by c(0). The sender sends the IV to the receiver in cleartext.

2. For the first block, the sender calculates m(1)⊕c(0), that is, calculates the exclusive-or of the first block of cleartext with the IV. It then runs the result through the block-cipher algorithm to get the corresponding ciphertext block; that is, c(1)=KS(m(1)⊕c(0)). The sender sends the encrypted block c(1) to the receiver.

3. For the ith block, the sender generates the ith ciphertext block from c(i)= KS(m(i)⊕c(i-1)).

Let’s now examine some of the consequences of this approach. First, the receiver will still be able to recover the original message. Indeed, when the receiver receives c(i), it decrypts it with KS to obtain s(i)=m(i)⊕c(i-1); since the receiver also knows c(i-1), it then obtains the cleartext block from m(i)=s(i)⊕c(i-1). Second, even if two cleartext blocks are identical, the corresponding ciphtertexts (almost always) will be different. Third, although the sender sends the IV in the clear, an intruder will still not be able to decrypt the ciphertext blocks, since the intruder does not know the secret key, S. Finally, the sender only sends one overhead block (the IV), thereby negligibly increasing the bandwidth usage for long messages (consisting of hundreds of blocks).

As an example, let’s now determine the ciphertext for the 3-bit block cipher in Table 8.1 with plaintext 010010010 and IV=c(0)=001. The sender first uses the IV to calculate c(1)=KS(m(1)⊕c(0))=100. The sender then calculates c(2)= KS(m(2)⊕c(1))=KS(010⊕100)=000, and C(3)=KS(m(3)⊕c(2))=KS(010⊕000)=101. The reader should verify that the receiver, knowing the IV and KS can recover the original plaintext.

CBC has an important consequence when designing secure network protocols: we’ll need to provide a mechanism within the protocol to distribute the IV from sender to receiver. We’ll see how this is done for several protocols later in this chapter.

8.2.2 公钥加密 6048.3 消息完整性与数字签名

8.2.2 Public Key Encryption 6048.3 Message Integrity and Digital Signatures

在长达两千多年的时间里（从凯撒密码时代直到 20 世纪 70 年代），加密通信都要求通信双方共享一个共同的秘密 —— 用于加密和解密的对称密钥。这种方法的一个难点是通信双方必须以某种方式达成对共享密钥的共识；但要做到这一点本身就需要（被认为是安全的）通信！或许双方可以先面对面会面达成密钥协议（例如，两个凯撒的百夫长可能在罗马浴场见面），此后再进行加密通信。然而，在网络化的世界中，通信双方可能永远不会见面，甚至无法通过除网络外的任何方式交流。那么，是否可能在没有事先已知共享密钥的情况下，仍能进行加密通信？1976 年，Diffie 和 Hellman [Diffie 1976] 提出了一种算法（现在称为 Diffie-Hellman 密钥交换）来实现这一目标 —— 这是一个完全不同且极其优雅的方法，开创了今天公钥密码系统的发展。不久后我们将看到，公钥密码系统还有几个极其出色的特性，使其不仅适用于加密，还适用于身份验证与数字签名。有趣的是，最近有资料显示，与 [Diffie 1976] 和 [RSA 1978] 中的思想相似的概念，早在 1970 年代初期，英国通信电子安全小组的研究人员就已经在一系列秘密报告中独立提出 [Ellis 1987]。正如常见的情况一样，伟大的想法往往会在不同地方独立诞生；幸运的是，公钥密码的突破不仅出现在私下，也得以在公众视野中发展。

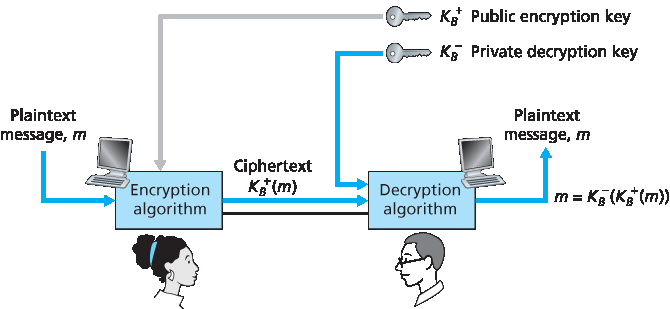
图 8.6 公钥密码学

公钥密码的使用在概念上相当简单。假设 Alice 想与 Bob 通信。如 图 8.6 所示，不同于对称密钥系统中 Bob 和 Alice 共享一个秘密密钥的方式，Bob（Alice 消息的接收者）拥有两个密钥 —— 一个 公钥，它对全世界都是公开的（包括入侵者 Trudy），以及一个仅 Bob 自己知道的 私钥。我们将分别用 \(K_B^+\) 和 \(K_B^-\) 表示 Bob 的公钥和私钥。为了与 Bob 通信，Alice 首先获取 Bob 的公钥。然后 Alice 使用 Bob 的公钥和一个已知的（例如标准化的）加密算法将消息 m 加密发送给 Bob；也就是说，Alice 计算 \(K_B^+(m)\)。Bob 收到 Alice 加密的消息后，使用他的私钥和一个已知的（例如标准化的）解密算法解密该加密消息。也就是说，Bob 计算 \(K_B^-(K_B^+(m))\)。我们将在下文看到，存在这样的加密/解密算法以及公私钥选择方法，使得 \(K_B^-(K_B^+(m))=m\) ；也就是说，对消息 m 应用 Bob 的公钥 \(K_B^+\) （得到 \(K_B^+(m)\) ），再应用 Bob 的私钥 \(K_B^-\) （即计算 \(K_B^-(K_B^+(m)）\) ）可以还原出 m。这是一个惊人的结果！通过这种方式，Alice 可以使用 Bob 公开可得的公钥向 Bob 发送秘密消息，而无需两人之间分发任何秘密密钥！我们很快将看到，可以交换公钥和私钥的加密操作，依然能得到同样惊人的结果 —— 即 \(K_B^-(K_B^+(m)) = K_B^+(K_B^-(m)) = m\) 。

因此，公钥加密在概念上是简单的。但人们也许会立刻想到两个问题。第一个担忧是，尽管入侵者拦截了 Alice 的加密消息只能看到乱码，但入侵者知道密钥（Bob 的公钥，对全世界公开）以及 Alice 用于加密的算法。Trudy 因此可以发动 选择明文攻击 ，使用已知的标准加密算法和 Bob 的公钥来对任意她想选择的消息进行加密！例如，Trudy 可能尝试加密她怀疑 Alice 会发送的消息内容或部分内容。显然，如果公钥加密系统要发挥作用，密钥选择和加密/解密的实现必须确保入侵者无法（或几乎不可能）推断出 Bob 的私钥，或以其他方式解密或猜测 Alice 给 Bob 的消息。第二个担忧是，既然 Bob 的加密密钥是公开的，任何人都可以向 Bob 发送加密消息，包括 Alice 或伪装成 Alice 的人。在共享密钥方案中，发送者知道密钥本身就能隐含地确认其身份。而在公钥加密中，这种情况不复存在，因为任何人都可以使用 Bob 的公钥向他发送加密消息。我们将在 第 8.3 节 中研究一个主题 —— 数字签名，它可用于将发送者与消息绑定起来。

For more than 2,000 years (since the time of the Caesar cipher and up to the 1970s), encrypted communication required that the two communicating parties share a common secret—the symmetric key used for encryption and decryption. One difficulty with this approach is that the two parties must somehow agree on the shared key; but to do so requires (presumably secure) communication! Perhaps the parties could first meet and agree on the key in person (for example, two of Caesar’s centurions might meet at the Roman baths) and thereafter communicate with encryption. In a networked world, however, communicating parties may never meet and may never converse except over the network. Is it possible for two parties to communicate with encryption without having a shared secret key that is known in advance? In 1976, Diffie and Hellman [Diffie 1976] demonstrated an algorithm (known now as Diffie-Hellman Key Exchange) to do just that—a radically different and marvelously elegant approach toward secure communication that has led to the development of today’s public key cryptography systems. We’ll see shortly that public key cryptography systems also have several wonderful properties that make them useful not only for encryption, but for authentication and digital signatures as well. Interestingly, it has recently come to light that ideas similar to those in [Diffie 1976] and [RSA 1978] had been independently developed in the early 1970s in a series of secret reports by researchers at the Communications-Electronics Security Group in the United ­Kingdom [Ellis 1987]. As is often the case, great ideas can spring up independently in many places; fortunately, public key advances took place not only in private, but also in the public view, as well.

Figure 8.6 Public key cryptography

The use of public key cryptography is conceptually quite simple. Suppose Alice wants to communicate with Bob. As shown in Figure 8.6, rather than Bob and Alice sharing a single secret key (as in the case of symmetric key systems), Bob (the recipient of Alice’s messages) instead has two keys—a public key that is available to everyone in the world (including Trudy the intruder) and a private key that is known only to Bob. We will use the notation KB+ and KB- to refer to Bob’s public and private keys, respectively. In order to communicate with Bob, Alice first fetches Bob’s public key. Alice then encrypts her message, m, to Bob using Bob’s public key and a known (for example, standardized) encryption algorithm; that is, Alice computes KB-(m). Bob receives Alice’s encrypted message and uses his private key and a known (for example, standardized) decryption algorithm to decrypt Alice’s encrypted message. That is, Bob computes KB-(KB+(m)). We will see below that there are encryption/decryption algorithms and techniques for choosing public and private keys such that KB-(KB+(m))=m; that is, applying Bob’s public key, KB+, to a message, m (to get KB-(m)), and then applying Bob’s private key, KB-, to the encrypted version of m (that is, computing KB-(KB+(m))) gives back m. This is a remarkable result! In this manner, Alice can use Bob’s publicly available key to send a secret message to Bob without either of them having to distribute any secret keys! We will see shortly that we can interchange the public key and private key encryption and get the same remarkable result––that is, KB-(B+(m))=KB+(KB-(m))=m.

The use of public key cryptography is thus conceptually simple. But two immediate worries may spring to mind. A first concern is that although an intruder intercepting Alice’s encrypted message will see only gibberish, the intruder knows both the key (Bob’s public key, which is available for all the world to see) and the algorithm that Alice used for encryption. Trudy can thus mount a chosen-plaintext attack, using the known standardized encryption algorithm and Bob’s publicly available encryption key to encode any message she chooses! Trudy might well try, for example, to encode messages, or parts of messages, that she suspects that Alice might send. Clearly, if public key cryptography is to work, key selection and encryption/decryption must be done in such a way that it is impossible (or at least so hard as to be nearly impossible) for an intruder to either determine Bob’s private key or somehow otherwise decrypt or guess Alice’s message to Bob. A second concern is that since Bob’s encryption key is public, anyone can send an encrypted message to Bob, including Alice or someone claiming to be Alice. In the case of a single shared secret key, the fact that the sender knows the secret key implicitly identifies the sender to the receiver. In the case of public key cryptography, however, this is no longer the case since anyone can send an encrypted message to Bob using Bob’s publicly available key. A digital signature, a topic we will study in Section 8.3, is needed to bind a sender to a message.

RSA

虽然有很多算法可以解决上述担忧，但 RSA 算法 （以其创始人 Ron Rivest、Adi Shamir 和 Leonard Adleman 命名）几乎已经成为公钥密码学的代名词。我们先看看 RSA 是如何工作的，然后再探究它为何可行。

RSA 广泛使用模 n 算术运算。因此，我们先简要回顾一下模运算。回忆一下， x mod n 表示 x 除以 n 后的余数；例如， 19 mod 5=4。在模运算中，可以进行加法、乘法和乘方等通常的运算。然而，每次运算的结果都被替换为其除以 n 后的整数余数。以下是一些有用的模运算规则，可以方便加法和乘法的运算：

[(a mod n)+(b mod n)] mod n = (a+b) mod n

[(a mod n)-(b mod n)] mod n = (a-b) mod n

[(a mod n)⋅(b mod n)] mod n = (a⋅b) mod n

由第三条可得 \((a \space \text{mod} \space n)^d \space \text{mod} \space n = a^d \space \text{mod} \space n\) ，这是我们即将频繁使用的恒等式。

现在假设 Alice 想给 Bob 发送一条 RSA 加密的消息，如 图 8.6 所示。在讨论 RSA 的过程中，请牢记消息不过是一个位模式，而每个位模式都可以唯一地用一个整数（以及位模式长度）表示。例如，假设消息是位模式 1001；它可以用十进制整数 9 表示。因此，在使用 RSA 加密消息时，等价于加密表示该消息的唯一整数。

RSA 包含两个相关的组成部分：

• 公钥和私钥的选择

• 加密与解密算法

为了生成 RSA 公钥和私钥，Bob 执行以下步骤：

1. 选择两个大素数 p 和 q。 p 和 q 应该多大？值越大，破解 RSA 的难度越大，但编码和解码所需的时间也越长。RSA 实验室建议 p 和 q 的乘积应约为 1024 位。关于如何寻找大素数，参见 [Caldwell 2012]。

2. 计算 n = pq， z=(p-1)(q-1)。

3. 选择一个小于 n 的数 e，它与 z 没有公因数（除了 1）。在这种情况下， e 和 z 被称为互素。字母 e 用来表示该值用于加密。

4. 找到一个数 d，使得 ed-1 能被 z 整除（即无余数）。字母 d 用来表示该值用于解密。换句话说，给定 e，选择 d 使得 ed mod z = 1。

5. Bob 对外公开的公钥 \(K_B^+\) 是数对 (n, e)；他的私钥 \(K_B^-\) 是数对 (n, d)。

Alice 的加密与 Bob 的解密过程如下：

• 假设 Alice 想要发送一个整数 m（m < n） 所表示的位模式给 Bob。为编码该消息，Alice 计算 m 的 e 次幂，然后取该结果除以 n 的余数。换句话说，Alice 明文 m 的密文值 c 为： c = m^e mod n。对应于密文 c 的位模式被发送给 Bob。

• 为了解密收到的密文 c，Bob 计算： m = c^d mod n

该操作需要使用他的私钥 (n, d)。

表 8.2 Alice 的 RSA 加密，e=5，n=35

明文字母	m: 数值表示	\(m^e\)	密文 c = m^e mod n
l	12	248832	17
o	15	759375	15
v	22	5153632	22
e	5	3125	10

作为一个简单的 RSA 示例，假设 Bob 选择 p=5 和 q=7 （诚然，这两个数过小，安全性极差）。则 n=35， z=24。Bob 选择 e=5，因为 5 与 24 没有公因数。最终，Bob 选择 d=29，因为 5⋅29-1 （即 ed-1）能被 24 整除。Bob 对外公开 n=35 和 e=5，并将 d=29 保密。已知这两个公开值，假设 Alice 现在想向 Bob 发送字母 l、o、v 和 e。将每个字母解释为 1 到 26 之间的数字（a 为 1，z 为 26），Alice 和 Bob 执行如 表 8.2 和 表 8.3 所示的加密和解密操作。注意，在这个示例中，我们将这四个字母各自作为独立的消息。一个更真实的示例会将这四个字母转换为其 8 位 ASCII 表示，再加密对应的 32 位位模式整数。（这种真实示例将产生过大而难以在教科书中打印的数字！）

鉴于 表 8.2 和 表 8.3 中这个“玩具”示例已经产生了极大的数字，同时我们也知道 p 和 q 应该是几百位长，由此引出几个关于 RSA 的实际问题。如何选择大素数？之后如何选择 e 和 d？如何对大数进行快速乘方计算？这些重要问题超出了本书的范围；请参阅 [Kaufman 1995] 及其参考资料以获取详细信息。

表 8.3 Bob 的 RSA 解密，d=29，n=35

密文 c	\(c^d\)	\(m = c^d mod n\)	明文字母
17	4819685721067509150915091411825223071697	12	l
15	127834039403948858939111232757568359375	15	o
22	851643319086537701956194499721106030592	22	v
10	1000000000000000000000000000000	5	e

While there may be many algorithms that address these concerns, the RSA Aalgorithm (named after its founders, Ron Rivest, Adi Shamir, and Leonard Adleman) has become almost synonymous with public key cryptography. Let’s first see how RSA works and then examine why it works.

RSA makes extensive use of arithmetic operations using modulo-n arithmetic. So let’s briefly review modular arithmetic. Recall that x mod n simply means the remainder of x when divided by n; so, for example, 19 mod 5=4. In modular arithmetic, one performs the usual operations of addition, multiplication, and exponentiation. However, the result of each operation is replaced by the integer remainder that is left when the result is divided by n. Adding and multiplying with modular arithmetic is facilitated with the following handy facts:

[ (a mod n)+(b mod n)]mod n=(a+b)mod n[ (a mod n)-(b mod n)]mod n=(a-b)mod n[ (a mod n)⋅(b mod n)]mod n=(a⋅b) mod n

It follows from the third fact that (a mod n)d n=ad mod n, which is an identity that we will soon find very useful.

Now suppose that Alice wants to send to Bob an RSA-encrypted message, as shown in Figure 8.6. In our discussion of RSA, let’s always keep in mind that a message is nothing but a bit pattern, and every bit pattern can be uniquely represented by an integer number (along with the length of the bit pattern). For example, suppose a message is the bit pattern 1001; this message can be represented by the decimal integer 9. Thus, when encrypting a message with RSA, it is equivalent to encrypting the unique integer number that represents the message.

There are two interrelated components of RSA:

• The choice of the public key and the private key

• The encryption and decryption algorithm

To generate the public and private RSA keys, Bob performs the following steps:

1. Choose two large prime numbers, p and q. How large should p and q be? The larger the values, the more difficult it is to break RSA, but the longer it takes to perform the encoding and decoding. RSA Laboratories recommends that the product of p and q be on the order of 1,024 bits. For a discussion of how to find large prime numbers, see [Caldwell 2012].

2. Compute n=pq and z=(p-1)(q-1).

3. Choose a number, e, less than n, that has no common factors (other than 1) with z. (In this case, e and z are said to be relatively prime.) The letter e is used since this value will be used in encryption.

4. Find a number, d, such that ed-1 is exactly divisible (that is, with no ­remainder) by z. The letter d is used because this value will be used in decryption. Put another way, given e, we choose d such that ed modz=1

5. The public key that Bob makes available to the world, KB+, is the pair of numbers (n, e); his private key, KB-, is the pair of numbers (n, d).

The encryption by Alice and the decryption by Bob are done as follows:

• Suppose Alice wants to send Bob a bit pattern represented by the integer number m (with m<n). To encode, Alice performs the exponentiation me, and then computes the integer remainder when me is divided by n. In other words, the encrypted value, c, of Alice’s plaintext message, m, is c=memod n The bit pattern corresponding to this ciphertext c is sent to Bob.

• To decrypt the received ciphertext message, c, Bob computes m=cdmod n

which requires the use of his private key (n, d).

Table 8.2 Alice’s RSA encryption, e=5, n=35

Plaintext Letter	m: numeric representation	\(m^e\)	Ciphertext c=me mod n
l	12	248832	17
o	15	759375	15
v	22	5153632	22
e	5	3125	10

As a simple example of RSA, suppose Bob chooses p=5 and q=7. ­(Admittedly, these values are far too small to be secure.) Then n=35 and z=24. Bob chooses e=5, since 5 and 24 have no common factors. Finally, Bob chooses d=29, since 5⋅29-1 (that is, ed-1) is exactly divisible by 24. Bob makes the two values, n=35 and e=5, public and keeps the value d=29 secret. Observing these two public values, suppose Alice now wants to send the letters l, o, v, and e to Bob. Interpreting each letter as a number between 1 and 26 (with a being 1, and z being 26), Alice and Bob perform the encryption and decryption shown in Tables 8.2 and 8.3, respectively. Note that in this example, we consider each of the four letters as a distinct message. A more realistic example would be to convert the four letters into their 8-bit ASCII representations and then encrypt the integer corresponding to the resulting 32-bit bit pattern. (Such a realistic example generates numbers that are much too long to print in a textbook!)

Given that the “toy” example in Tables 8.2 and 8.3 has already produced some extremely large numbers, and given that we saw earlier that p and q should each be several hundred bits long, several practical issues regarding RSA come to mind. How does one choose large prime numbers? How does one then choose e and d? How does one perform exponentiation with large numbers? A discussion of these important issues is beyond the scope of this book; see [Kaufman 1995] and the references therein for details.

Table 8.3 Bob’s RSA decryption, d=29, n=35

Ciphertext c	\(c^d\)	\(m = c^d mod n\)	Plaintext Letter
17	4819685721067509150915091411825223071697	12	l
15	127834039403948858939111232757568359375	15	o
22	851643319086537701956194499721106030592	22 v	v
10	1000000000000000000000000000000	5	e

会话密钥

Session Keys

我们在此指出，RSA 所需的幂运算是一个相当耗时的过程。相比之下，DES 在软件中至少快 100 倍，在硬件中则快 1,000 到 10,000 倍 [RSA Fast 2012]。因此，在实际应用中，RSA 通常与对称密钥密码算法结合使用。例如，如果 Alice 想要向 Bob 发送大量加密数据，她可以这样做：首先，Alice 选择一个用于加密数据本身的密钥；这个密钥被称为 会话密钥，记作 \(K_S\) 。由于这是他们将与对称密钥加密算法（例如 DES 或 AES）一起使用的共享密钥，Alice 必须将会话密钥告知 Bob。Alice 使用 Bob 的公钥加密会话密钥，即计算 \(c = (K_S)^e \space \text{mod} \space n\) 。Bob 接收到 RSA 加密的会话密钥 c 后，解密得到会话密钥 \(K_S\)。至此，Bob 已知 Alice 将用于加密数据传输的会话密钥。

We note here that the exponentiation required by RSA is a rather time-consuming process. By contrast, DES is at least 100 times faster in software and between 1,000 and 10,000 times faster in hardware [RSA Fast 2012]. As a result, RSA is often used in practice in combination with symmetric key cryptography. For example, if Alice wants to send Bob a large amount of encrypted data, she could do the following. First Alice chooses a key that will be used to encode the data itself; this key is referred to as a session key, and is denoted by KS. Alice must inform Bob of the session key, since this is the shared ­symmetric key they will use with a symmetric key cipher (e.g., with DES or AES). Alice encrypts the session key using Bob’s public key, that is, computes c=(KS)e mod n. Bob receives the RSA-encrypted session key, c, and decrypts it to obtain the session key, KS. Bob now knows the session key that Alice will use for her encrypted data transfer.

RSA 为何有效？

Why Does RSA Work?

RSA 的加解密过程似乎相当神奇。为何在应用加密算法后再应用解密算法，就能恢复原始消息？为了理解 RSA 的原理，我们再次记 n = pq，其中 p 和 q 是用于 RSA 算法中的两个大素数。

回忆一下，在 RSA 加密中，一个消息（可以唯一表示为一个整数） m 被提升到 e 次幂，并使用模 n 运算，即：

\[c = m^e \space \text{mod} \space n\]

解密则是将该值提升到 d 次幂，同样使用模 n 运算。因此，加密步骤后接解密步骤的结果为 (m^e mod n)^d mod n。现在我们来看一下这个表达式的含义。如前所述，模运算的一个重要性质是 (a mod n)^d mod n = a^d mod n，对于任意 a、n、d 都成立。因此，令 a = m^e 应用于该性质，我们有：

\[(m^e \space \text{mod} \space n)^d \space \text{mod} \space n = \space m^{e⋅d} \space \text{mod} \space n\]

因此我们只需证明 \(m^{e⋅d} \space \text{mod} \space n = m\)。虽然我们试图揭开 RSA 的神秘面纱，但为证明这一点，我们需要引用一个来自数论的“神奇”定理。具体来说，该定理指出，如果 p 和 q 是素数， n = pq，且 z = (p-1)(q-1)，那么：\(x^y \space \text{mod} \space n\) 与 \(x^{(y \space \text{mod} \space z)} \space \text{mod} \space n\) 相等 [Kaufman 1995]。将该结论应用于 x = m, y = e⋅d，我们得到：

\[m^{e⋅d} \space \text{mod} \space n = m^{(e⋅d \space \text{mod} \space z)} \space \text{mod} \space n\]

而我们已知选择 e 和 d 满足 e⋅d mod z = 1。因此：

\[m^{e⋅d} \space \text{mod} \space n = m^1 \space \text{mod} \space n \space = \space m\]

这正是我们想要的结果！先执行 e 次幂运算（即加密），然后执行 d 次幂运算（即解密），即可恢复原始值 m。更令人惊奇的是，如果我们先执行 d 次幂运算，然后再执行 e 次幂运算——即先解密再加密——我们也能得到原始值 m。这一奇妙结果直接源于模运算的性质：

\[(m^d \space \text{mod} \space n)^e \space \text{mod} \space n = m^{(d⋅e)} \space \text{mod} \space n = m^{(e⋅d)} \space \text{mod} \space n = (m^e \space \text{mod} \space n)^d \space \text{mod} \space n\]

RSA 的安全性依赖于一个事实：目前尚无快速算法可将一个数（即公开值 n）分解为其素因数 p 和 q。如果知道了 p 和 q，那么给定公开值 e，就可以轻松计算出私钥 d。另一方面，目前尚不清楚是否存在快速因数分解算法，因此从这个意义上说，RSA 的安全性并非绝对保证。

另一个流行的公钥加密算法是 Diffie-Hellman 算法，我们将在习题中简要探讨。与 RSA 不同，Diffie-Hellman 不具备加密任意长度消息的能力；但它可以用于建立一个对称会话密钥，而该密钥随后可用于加密消息。

RSA encryption/decryption appears rather magical. Why should it be that by applying the encryption algorithm and then the decryption algorithm, one recovers the original message? In order to understand why RSA works, again denote n=pq, where p and q are the large prime numbers used in the RSA algorithm.

Recall that, under RSA encryption, a message (uniquely represented by an ­integer), m, is exponentiated to the power e using modulo-n arithmetic, that is,

c=memod n

Decryption is performed by raising this value to the power d, again using modulo-n arithmetic. The result of an encryption step followed by a decryption step is thus (me mod n)d mod n. Let’s now see what we can say about this quantity. As mentioned earlier, one important property of modulo arithmetic is (a mod n)d mod n=ad mod n for any values a, n, and d. Thus, using a=me in this property, we have

(memod n)dmod n=medmod n

It therefore remains to show that medmod n=m. Although we’re trying to remove some of the magic about why RSA works, to establish this, we’ll need to use a rather magical result from number theory here. Specifically, we’ll need the result that says if p and q are prime, n=pq, and z=(p-1)(q-1), then \(x^y\) mod n is the same as \(x^{(y mod z)} mod n\) [Kaufman 1995]. Applying this result with x=m and y=ed we have

medmod n=m(edmod z)mod n

But remember that we have chosen e and d such that edmod z=1. This gives us

medmod n=m1mod n=m

which is exactly the result we are looking for! By first exponentiating to the power of e (that is, encrypting) and then exponentiating to the power of d (that is, ­decrypting), we obtain the original value, m. Even more wonderful is the fact that if we first exponentiate to the power of d and then exponentiate to the power of e—that is, we reverse the order of encryption and decryption, performing the decryption operation first and then applying the encryption operation—we also obtain the original value, m. This wonderful result follows immediately from the modular arithmetic:

(mdmod n)emod n=mdemod n=medmod n=(memod n)dmod n

The security of RSA relies on the fact that there are no known algorithms for quickly factoring a number, in this case the public value n, into the primes p and q. If one knew p and q, then given the public value e, one could easily compute the secret key, d. On the other hand, it is not known whether or not there exist fast algorithms for factoring a number, and in this sense, the security of RSA is not guaranteed.

Another popular public-key encryption algorithm is the Diffie-Hellman algorithm, which we will briefly explore in the homework problems. Diffie-Hellman is not as versatile as RSA in that it cannot be used to encrypt messages of arbitrary length; it can be used, however, to establish a symmetric session key, which is in turn used to encrypt messages.